時空 解 さんの日記
2018
8月
13
(月)
10:10
本文
皆さん、おはようございます。時空 解です。
数学検定が終わって早20日間が過ぎてしまっています。今までは青チャート「改訂版 チャート式 基礎からの 数学I+A」の数学Iの第4章:図形と計量のところの18節 "正弦定理と余弦定理" で戸惑っていたのですが、ここの Exercises も終わり、やっと一区切り付きましたので、これからは数学Aの第1章、場合の数に進むことにしました。と言うのも、数学検定2級を過去3回受検して、「自分は "場合の数" と "確率" が弱いな」と思っからです。
と言うことで、昨日さっそく青チャート「改訂版 チャート式 基礎からの 数学I+A」の p296 から手を付けた次第です。
「始めの方は、基礎だから簡単だろうな…」
そう思いながら、大阪から帰ってきたばかりの夜にチャチャチャと2、3ページくらいは学習を進めようと思って取り掛かったのですが…。
シヨックです!
下記の基本事項がスッとイメージできずになかなか手こずってしまったのです。
集合の個数定理、第3番目
3つの集合の和集合の要素の個数
$ n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)+n(A \cap B \cap C) $
上記の公式をみて、皆さんは最後の項 $ n(A \cap B \cap C) $ が何故必要なのか、すぐに分かりましたか?
私は「おやっ?」と、首をひねってしまいました。
表記方法はお分かりですかね?例えば集合 $ A $ の要素の個数は $ n(A) $ と表記します。
ですから上記の公式の、まず左辺 $ n(A \cup B \cup C) $ はベン図を使うと下記のようになります。
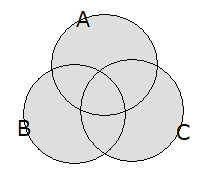
次に、右辺の各項は次のようになります。
最初の $ n(A)+n(B)+n(C) $ の項がポイントになります。加減算を円を重ねたり、取り払うイメージで説明しますので、そのつもりで見て下さいね。
$ n(A)+n(B)+n(C) $、 $ -n(A \cap B) $、 $ -n(B \cap C) $、 $ -n(C \cap A) $、 $ +n(A \cap B \cap C) $
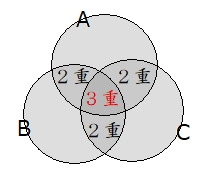
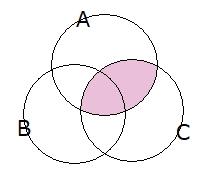
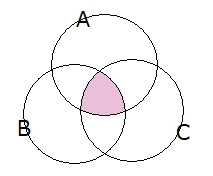
このようにベン図を書き並べるとイメージを持ちやすくなるのではないでしょうか?
最初の $ n(A)+n(B)+n(C) $ の項は、3つの円 $ A,B,C $ を重ねて行くと、真ん中の部分は3つ重なっている事が判りますよね。他の重なりの部分は2重になっているだけです。
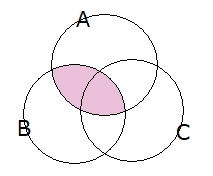
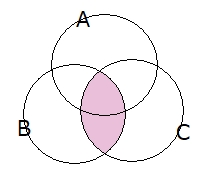
さて、引き算 $ -n(A \cap B),-n(B \cap C),-n(C \cap A) $ を行うとどうなるでしょう?これは2重の部分を1つ取り払いたいために行う引き算です。そうすると下図の3つの部分
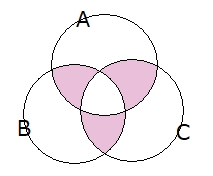
この部分は1回取り払われる事になるので、2重の部分を1つ取り払うことに成功しますが…真ん中のところは3回も取り払う事になります。真ん中の3重のところは2回取り払いたいだけなのにね。
ですから最後の項 $ +n(A \cap B \cap C) $ が必要になります。
青チャート「改訂版 チャート式 基礎からの 数学I+A」にこの個数定理の3番の証明が載っているのですが、数式の演算で行われていますのでイメージがつかみにくいです。( まぁ私だけか知れませんが )
Yahoo!知恵袋と言うところにも、同じような疑問をお持ちの方からの質問と、それに対する回答もありますが…
・3つの集合の個数定理
私のベン図を使った説明は、分かりやすかったでしょうか?
結構時間掛かってしまいましたので、分かってね。
とにかく、上記の説明内容が高校生の時だったら一瞬でイメージ出来たと思うのですが…社会人になるとおよそ数学とは縁が無くなりますからね、簡単な定理もパッとイメージ出来なくなるのでしょうかね…。
( あくまでも歳のせいではないと考えたい私でした )
では今日も1日の習慣を始めます。小さな一歩・挑戦を試みます。
数学検定が終わって早20日間が過ぎてしまっています。今までは青チャート「改訂版 チャート式 基礎からの 数学I+A」の数学Iの第4章:図形と計量のところの18節 "正弦定理と余弦定理" で戸惑っていたのですが、ここの Exercises も終わり、やっと一区切り付きましたので、これからは数学Aの第1章、場合の数に進むことにしました。と言うのも、数学検定2級を過去3回受検して、「自分は "場合の数" と "確率" が弱いな」と思っからです。
と言うことで、昨日さっそく青チャート「改訂版 チャート式 基礎からの 数学I+A」の p296 から手を付けた次第です。
「始めの方は、基礎だから簡単だろうな…」
そう思いながら、大阪から帰ってきたばかりの夜にチャチャチャと2、3ページくらいは学習を進めようと思って取り掛かったのですが…。
シヨックです!
下記の基本事項がスッとイメージできずになかなか手こずってしまったのです。
集合の個数定理、第3番目
3つの集合の和集合の要素の個数
$ n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)+n(A \cap B \cap C) $
上記の公式をみて、皆さんは最後の項 $ n(A \cap B \cap C) $ が何故必要なのか、すぐに分かりましたか?
私は「おやっ?」と、首をひねってしまいました。
表記方法はお分かりですかね?例えば集合 $ A $ の要素の個数は $ n(A) $ と表記します。
ですから上記の公式の、まず左辺 $ n(A \cup B \cup C) $ はベン図を使うと下記のようになります。

次に、右辺の各項は次のようになります。
最初の $ n(A)+n(B)+n(C) $ の項がポイントになります。加減算を円を重ねたり、取り払うイメージで説明しますので、そのつもりで見て下さいね。
$ n(A)+n(B)+n(C) $、 $ -n(A \cap B) $、 $ -n(B \cap C) $、 $ -n(C \cap A) $、 $ +n(A \cap B \cap C) $





このようにベン図を書き並べるとイメージを持ちやすくなるのではないでしょうか?
最初の $ n(A)+n(B)+n(C) $ の項は、3つの円 $ A,B,C $ を重ねて行くと、真ん中の部分は3つ重なっている事が判りますよね。他の重なりの部分は2重になっているだけです。
さて、引き算 $ -n(A \cap B),-n(B \cap C),-n(C \cap A) $ を行うとどうなるでしょう?これは2重の部分を1つ取り払いたいために行う引き算です。そうすると下図の3つの部分

この部分は1回取り払われる事になるので、2重の部分を1つ取り払うことに成功しますが…真ん中のところは3回も取り払う事になります。真ん中の3重のところは2回取り払いたいだけなのにね。
ですから最後の項 $ +n(A \cap B \cap C) $ が必要になります。
青チャート「改訂版 チャート式 基礎からの 数学I+A」にこの個数定理の3番の証明が載っているのですが、数式の演算で行われていますのでイメージがつかみにくいです。( まぁ私だけか知れませんが )
Yahoo!知恵袋と言うところにも、同じような疑問をお持ちの方からの質問と、それに対する回答もありますが…
・3つの集合の個数定理
私のベン図を使った説明は、分かりやすかったでしょうか?
結構時間掛かってしまいましたので、分かってね。
とにかく、上記の説明内容が高校生の時だったら一瞬でイメージ出来たと思うのですが…社会人になるとおよそ数学とは縁が無くなりますからね、簡単な定理もパッとイメージ出来なくなるのでしょうかね…。
( あくまでも歳のせいではないと考えたい私でした )
では今日も1日の習慣を始めます。小さな一歩・挑戦を試みます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 平日を充実させるために… | ☆ 実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) 朝食後 |
加減算 できず 1回 掛け算 できず |
| 斜め懸垂1回 (ボルダリングの体力獲得) &fnbsp; ブログ投稿後 |
できず |
| 数学の問題 1問 (物理学の数式の理解力の獲得) 9時15分~11時15分 ,2時間 |
チャート式 数学 白II+B:できず チャート式 数学 青I+A:p296~p297 数学の答え合わせは後でまとめてやる:× ( p244 の復習 ) 2時間は机から離れず、パソコンの画面も見ずに数学の学習に取り組む:× |
| 心の筋トレ (集中力の獲得) 習慣を実行するにあたって |
今朝・7時に布団から出る:7時55分 --- ブログの投稿 --- 昨日・朝食は台所でとって2階へ:〇 昨日・机に座ったら、直ぐに学習用具を開く:〇 昨日・寝床に入った時間:23時27分 |
閲覧(2869)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |






 前の日記
前の日記



