時空 解 さんの日記
2018
2月
8
(木)
10:45
本文
皆さん、おはようございます。時空 解です。
曲線 \(y = 2x^3 - 3x\) を C とする。
(1) C 上の点 \((a, 2a^3-3a)\) における C の接線の方程式を求めよ。
(2) (1) で求めた接線が点 \((1, b)\) を通るとき、 b を a の式で表せ。
(3) 点\((1, b)\) から C へ異なる3本の接線が引けるような b の値の範囲を求めよ。
上記の問題は、白チャート 数学II+B の p262, Exercises の 問題 385 なのですが、難しい問題でした。
何が難しいって、解法のテクニック自体は分かるにしても、そのテクニックを適用するとどうして解けるのか?それがピンと来ません。
私には未知の領域です。
でもねぇ…グラフを書いてみると正しいなぁと思うのです。
とにかく私に取ってこの問題は、「正しいんだね、これで…」と、徐々に納得して行くしかない代物でした。
この問題を一緒に見て行きましょう。
まずは (1) ですが、これは3次方程式をわざわざ C と置き換えて表現している事に振り回されなければ大丈夫です。曲線 \(y = 2x^3 - 3x\) 上にある点 \((a, 2a^3-3a)\) の接線の方程式を求めよ と言っているだけです。ですから接線の傾きが分れば、この接線が通る一つの点は \((a, 2a^3-3a)\) と分かっていますから、2次方程式を立てる事ができます。
まず接線はこの節のテーマでもある微分で導けますよね。次は、数学Iの "2次関数のグラフと移動" のところで2次関数の一般形と基本形と言うのがありましたが、これを思い出してみましょう。
一般形: \(y = ax^2 + bx + c\)
基本形: \(y = a(x - p)^2 + q\) → \(y - q = a(x - p)^2\)
この2つのうちの基本形を利用すれば、(1)が解けます。
点 \((a, 2a^3-3a)\) の \(a\) が基本形の p に、\(2a^3-3a\) が q に対応します。
( 実は上記がピンとくるようになったのは、数学Iの第3章 "2次関数" をちゃんと学習したからです。以前は私、基本形がピンと来ませんでした。 )
従って基本形に点 \((a, 2a^3-3a)\) を当てはめると
\( y - (2a^3 - 3a) = (6a^2 - 3)(x - a)\)
すなわち
\( y = (6a^2 - 3)x - 4a^3\)
となります。
次は (2) ですが、これも点\((1, b)\) が接線が通る、と言う事から分かります。(1) で求めた接線の方程式の x と y にそれぞれ 1 と b を代入して整理するだけです。\( y = (6a^2 - 3)x - 4a^3\) の x に 1、y に b を代入すると \( b = (6a^2 - 3)1 - 4a^3\) ですので、これを整理すると下記になります。
\( b = -4a^3 + 6a^2 - 3\)
さて、私が理解に苦しむのは次の (3) です。
(1) と (2) の問題は、実はこの (3) を解くためのステップだと何となくは分かるのですが…。すなわち (2) で求めた方程式から \( y = -4a^3 + 6a^2 - 3\) と \( y = b\) の交点が3つ存在するように b の値を見つければよいようだなぁ…とね。
でもこれが正しいと確信するには苦労しました。
でも確かに (1) の問いと (2) の問いを解いた時点で、C と 点\((1, b)\) を通るグラフは \( b = -4a^3 + 6a^2 - 3\) の形をしている事は導けているのです…。
とにかく、(3) は (1) と (2) の結果を受けて、下記の2つの方程式の交点が3つならば接線も3つある事になるのです。
\(f(a) = -4a^3 + 6a^2 - 3\)
\(f(a) = b\)
これが正しい事をグラフを書いてみて、確認して行きましょう。
上式 \(f(a) = -4a^3 + 6a^2 - 3\) をグラフで書くと下記のようになります。
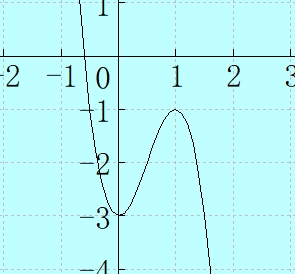
これに \(f(a) = -3\) と \(f(a) = -1\) を書き加えてみます。-3 と -1 と言うのは実は b の取りうる値、すなわち (3) の答えですよ。
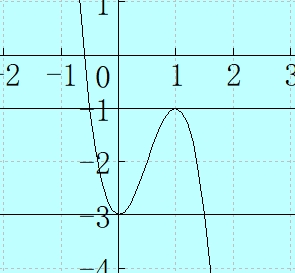
b がこの -1 から -3 の値の間ならば、曲線 \(f(a) = -4a^3 + 6a^2 - 3\) と3つの交点を持ちます。(3) の問題は「点\((1, b)\) から C へ異なる3本の接線が引けるような b の値の範囲」でしたよね。ですから点\((1, b)\) の b は \(-3 < b < -1\) です。これもグラフで確認してみましょう。
「グラフ C」 と「点\((1, b)\) の範囲 (赤線)」、点\((1, -1.2)\) 辺りから「グラフに三本の接線 (茶色線) 」の三つを下記に示します。
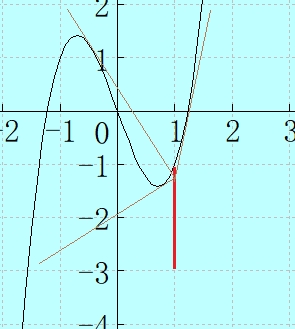
こうして接線を引いてみると確かに \(-3 < b < -1\) の範囲でなければ接線は三本引けない事が見て取れますよね。
ここまでしないと、私には納得の出来ない問題でした。
いやはや、今日はブログを書くにも時間が掛かってしまいましたが、こんな具合で LaTeX2ε、Mathjax を利用して数式を文章中に取り入れて行きますね。
グラフもそのうち LaTeX2ε、Mathjax を利用できればなぁ…と思っております。
では今日も1日の習慣は実施します。小さな一歩・挑戦を試みます…と言ってもちょっと時間が無くなってしまいましたね。出来る範囲で実施します。
曲線 \(y = 2x^3 - 3x\) を C とする。
(1) C 上の点 \((a, 2a^3-3a)\) における C の接線の方程式を求めよ。
(2) (1) で求めた接線が点 \((1, b)\) を通るとき、 b を a の式で表せ。
(3) 点\((1, b)\) から C へ異なる3本の接線が引けるような b の値の範囲を求めよ。
上記の問題は、白チャート 数学II+B の p262, Exercises の 問題 385 なのですが、難しい問題でした。
何が難しいって、解法のテクニック自体は分かるにしても、そのテクニックを適用するとどうして解けるのか?それがピンと来ません。
私には未知の領域です。
でもねぇ…グラフを書いてみると正しいなぁと思うのです。
とにかく私に取ってこの問題は、「正しいんだね、これで…」と、徐々に納得して行くしかない代物でした。
この問題を一緒に見て行きましょう。
まずは (1) ですが、これは3次方程式をわざわざ C と置き換えて表現している事に振り回されなければ大丈夫です。曲線 \(y = 2x^3 - 3x\) 上にある点 \((a, 2a^3-3a)\) の接線の方程式を求めよ と言っているだけです。ですから接線の傾きが分れば、この接線が通る一つの点は \((a, 2a^3-3a)\) と分かっていますから、2次方程式を立てる事ができます。
まず接線はこの節のテーマでもある微分で導けますよね。次は、数学Iの "2次関数のグラフと移動" のところで2次関数の一般形と基本形と言うのがありましたが、これを思い出してみましょう。
一般形: \(y = ax^2 + bx + c\)
基本形: \(y = a(x - p)^2 + q\) → \(y - q = a(x - p)^2\)
この2つのうちの基本形を利用すれば、(1)が解けます。
点 \((a, 2a^3-3a)\) の \(a\) が基本形の p に、\(2a^3-3a\) が q に対応します。
( 実は上記がピンとくるようになったのは、数学Iの第3章 "2次関数" をちゃんと学習したからです。以前は私、基本形がピンと来ませんでした。 )
従って基本形に点 \((a, 2a^3-3a)\) を当てはめると
\( y - (2a^3 - 3a) = (6a^2 - 3)(x - a)\)
すなわち
\( y = (6a^2 - 3)x - 4a^3\)
となります。
次は (2) ですが、これも点\((1, b)\) が接線が通る、と言う事から分かります。(1) で求めた接線の方程式の x と y にそれぞれ 1 と b を代入して整理するだけです。\( y = (6a^2 - 3)x - 4a^3\) の x に 1、y に b を代入すると \( b = (6a^2 - 3)1 - 4a^3\) ですので、これを整理すると下記になります。
\( b = -4a^3 + 6a^2 - 3\)
さて、私が理解に苦しむのは次の (3) です。
(1) と (2) の問題は、実はこの (3) を解くためのステップだと何となくは分かるのですが…。すなわち (2) で求めた方程式から \( y = -4a^3 + 6a^2 - 3\) と \( y = b\) の交点が3つ存在するように b の値を見つければよいようだなぁ…とね。
でもこれが正しいと確信するには苦労しました。
でも確かに (1) の問いと (2) の問いを解いた時点で、C と 点\((1, b)\) を通るグラフは \( b = -4a^3 + 6a^2 - 3\) の形をしている事は導けているのです…。
とにかく、(3) は (1) と (2) の結果を受けて、下記の2つの方程式の交点が3つならば接線も3つある事になるのです。
\(f(a) = -4a^3 + 6a^2 - 3\)
\(f(a) = b\)
これが正しい事をグラフを書いてみて、確認して行きましょう。
上式 \(f(a) = -4a^3 + 6a^2 - 3\) をグラフで書くと下記のようになります。

これに \(f(a) = -3\) と \(f(a) = -1\) を書き加えてみます。-3 と -1 と言うのは実は b の取りうる値、すなわち (3) の答えですよ。

b がこの -1 から -3 の値の間ならば、曲線 \(f(a) = -4a^3 + 6a^2 - 3\) と3つの交点を持ちます。(3) の問題は「点\((1, b)\) から C へ異なる3本の接線が引けるような b の値の範囲」でしたよね。ですから点\((1, b)\) の b は \(-3 < b < -1\) です。これもグラフで確認してみましょう。
「グラフ C」 と「点\((1, b)\) の範囲 (赤線)」、点\((1, -1.2)\) 辺りから「グラフに三本の接線 (茶色線) 」の三つを下記に示します。

こうして接線を引いてみると確かに \(-3 < b < -1\) の範囲でなければ接線は三本引けない事が見て取れますよね。
ここまでしないと、私には納得の出来ない問題でした。
いやはや、今日はブログを書くにも時間が掛かってしまいましたが、こんな具合で LaTeX2ε、Mathjax を利用して数式を文章中に取り入れて行きますね。
グラフもそのうち LaTeX2ε、Mathjax を利用できればなぁ…と思っております。
では今日も1日の習慣は実施します。小さな一歩・挑戦を試みます…と言ってもちょっと時間が無くなってしまいましたね。出来る範囲で実施します。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね)![]()
| ★ 習慣作りのための、小さな課題 | ☆ 昨日の実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿後 |
宮田 輝 そろばん教室 練習問題3、4、5 各2回 |
| 斜め懸垂1回 (ボルダリングの体力獲得) 朝食前 |
できず |
| チャート式参考書1問 (物理学の数式の理解力の獲得) 朝食後9時から |
白II+B:p262,ex-385 青I+A:出来ず |
| 心の筋トレ (集中力の獲得) 習慣を実行するにあたって |
今朝・7時に布団から出る:7時43分 --- ブログの投稿 --- 昨日・朝食は台所で摂って2階へ:× 昨日・机に座ったら、直ぐに学習用具を開く:〇 昨日・理数の解法を楽しむ:〇 昨日・夜食も台所で摂って2階に:× 昨日・夜は11時に布団にはいる:11時19分 |
閲覧(8078)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



