50代から理数を学ぶ - とっても難しいと思った空間のベクトル問題 EX-128

Home > ブログ > 時空解 > 数学 > とっても難しいと思った空間のベクトル問題 EX-128

時空解さんの日記

2019

5月 19

(日)

09:17

とっても難しいと思った空間のベクトル問題 EX-128

前の日記次の日記

カテゴリー数学

本文

皆さん、おはようございます。時空解です。

この２、３日のあいだ、数学の学習スピードが亀のような速度になっています。白チャート「新課程チャート式基礎と演習数学 II+B」の空間ベクトルのところを学習しているのですが、遅くなっている原因は空間ベクトルが難しいからです。

私に取ってね。

一度答えを見て「おお！なるほど」と思っても、いざやり直してみると分からない…　( x x);?

二度見てやり直してもベクトル数式の変形で書き間違い…

最近、普通の数式では計算式の書き間違い・計算間違いの類はだんだんと減ってきてるんですけどね。
きっと数学の問題を解く事に慣れてきたのだと思います。
でも、ベクトルとなるとまだまだ…やっぱりベクトルの数式に慣れていないせいでしょう。

この理由は、普通の数式は言語脳で処理するけど、ベクトルの数式は空間脳で処理する必要があるからかな？

おっと　

ま、そんなことは余計な考えですね。

さて、昨日難しいなぁと思った問題がこちらです。

白チャート「新課程チャート式基礎と演習数学 II+B」p381 の EX128

四面体 $OABC$ の辺 $OA,~OC$ の中点をそれぞれ $L,~M$ とし、辺 $AB$ を $2:1$ に内分する点を $R$ とする。また、辺 $OB$ を $2:1$ に外分する点を $N$ とし、直線 $BC$ と直線 $NM$ の交点を $S$ とする。
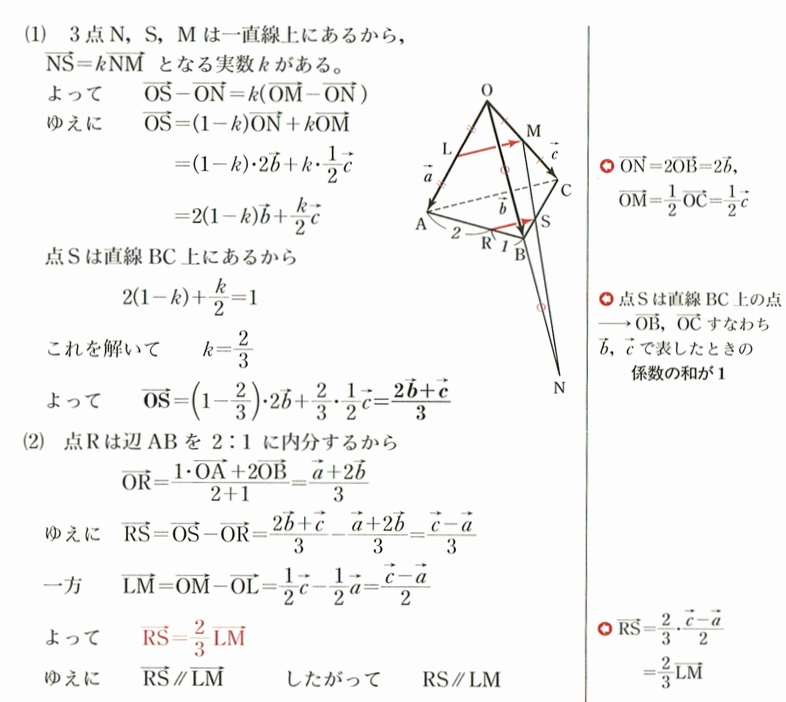
(1) $\vec{ OA } = \vec{ a },~ \vec{ OB }= \vec{ b },~ \vec{ OC }= \vec{ c }$ とするとき、 $\vec{ OS }$ を $\vec{ a },~ \vec{ b },~ \vec{ c }$ を用いて表せ。
(2) $RS /\!/ LM$ であることを証明せよ。

この問題は、まず与えられた問題の図を正しく描くことがなかなか難しいですよね。内分と外分が出て来ますから。でもこの辺はちゃんと学習していれば問題はありません。
難しいと想えるのは、線分

$BC$ 上にある点

$S$ の位置ですよね。

$BC$ の中点だと分かっているのならば簡単です。

$\vec{ s } = \vec{ OS } = \displaystyle \frac{ \vec{ b } + \vec{ c } }{ 2 }$

ですからね。

でも点

$S$ は中点ではありません。この位置をどう計算するか？　ここが問題です。

では答えを見てみましょう。

うーむ、エレガントな解答です。

$〇 \cdot \vec{ b } + △ \cdot \vec{ c }$ と言う形に持って行って、点

$b,~s,~c$ が一直線上にあることから

$〇 + △ = 1$ と言う式を立てて

$k$ を求めるところがポイントでしょう。

今日また夜、復習することにします。

では今日も１日の習慣を始めます。小さな一歩・挑戦を試みます。

応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは１日にして成らず、です。

(ポチッとブログ村のバナーをクリックしてね）

「小さな習慣 ( 良い習慣化計画 ) 」の実施状況
★ 習慣作りのための、小さな課題	☆ 実施状況
２階に上り降り時、懸垂１回 (ボルダリングの体力獲得) 学習の気分転換	グリップ４０回、腕立て２０回、腹筋２０回、完全懸垂２回、縄跳び６０回
そろばんの練習５問 (暗算の獲得) 数学の学習前	加減算１１～１１０の足し算１回、１１～１１０の引き算１回乗算せず
数学の問題１問 (物理学の数式の理解力の獲得) ９０分	チャート式数学白II+B：p381,ex128 チャート式数学青I+A：せず実用数学技能検定要点整理２級：せず数学の答え合わせは後でまとめてやる：〇数学の学習に取り組んだ時間：40分
規則正しい生活基本習慣	昨日・寝床に入った時間：２３時５０分今朝・７時に布団から出る：７時１６分朝 --- ブログの投稿 ---

閲覧(7810)

コメントを書く
コメントを書くにはログインが必要です。