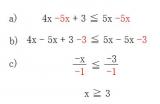時空 解 さんの日記
みなさん、こんにちは。
数学の不等式の問題を解いていて、ふと迷い、二時間くらいその問題を解決する事が出来ませんでした。
みなさんは下記の不等式をみて、 x の値を求める事はひとまず横に置いておいて、「計算式の移行」に付いてハタと疑問を持ったりはしませんかねぇ…。
・4x + 3 ≦ 5x ≦ x - 4
この問題の解法として数学の参考書には、上の与式を2つに分けて計算する方法が示されています。
① 4x + 3 ≦ 5x
② 5x ≦ x - 4
上記のように2つに分けて計算するわけです。①と②、どちらを演算するにも、まずは左辺に x をまとめる事を考えますよね。そうすると①の式は
a) 5x を右辺から左辺へ移行して、
b) 次に 3 を左辺から右辺に移行し、
c) 最後に -1 で割ります。
となります。この一連のようすを下記に示します。

さて、ここでハタと思ったのですが、そもそもの与式は 4x + 3 ≦ 5x ≦ x - 4 と言うことなので、真ん中の 5x を右側に移行するのと左側に移行するのと、好き勝手にやってもいいのだろうか?と言う疑問が湧いてしまいました。そして数学の参考書の説明のように、与式 4x + 3 ≦ 5x ≦ x - 4 は2つに分けて考えて良いものなのだろうか?参考書が間違ってないかぁ!?と思ってしまいました。
この疑いの気分を払拭するのに、2時間かかってしまいました。いやはや、数式解法のテクニック「移行」と言う事の本質を忘れて技法だけが頭に残っていたのですねぇ。
本来の意味が分かるように①の式を変形すると下記になります。
a) 両辺に -5x を加える。
b) 次に両辺に -3 を加える。
c) 最後に両辺を -1 で割ります。(大小符号は -1 で割る時は逆転します)

これならば不等号が2つある与式 4x + 3 ≦ 5x ≦ x - 4 にでも矛盾なく処理を行なえます。
分かってしまえば簡単な事なのに、2時間嵌ってしまうなんて・・・思い込みとは恐ろしい物です。
では今日はこの辺で。
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記