時空 解 さんの日記
2019
9月
8
(日)
09:48
本文
皆さん、おはようございます。時空 解です。
今日は朝から町内会で公園の草取りでした。疲れましたぁ~。草を取る公園が自宅の目と鼻の先にあるものですから休む訳にはゆきません。
トップリ疲れていますが、今日は四苦八苦して理解したチェバの定理について書いてみます。
トップリ疲れていますが、今日は四苦八苦して理解したチェバの定理について書いてみます。
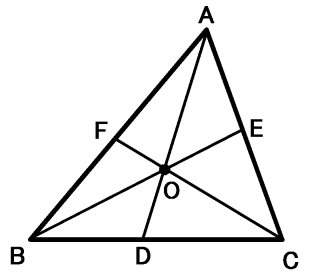
チェバの定理 ( Wikipedia へリンク )
$ \displaystyle { {AF \over FB}\cdot {BD \over DC}\cdot {CE \over EA}=1 } $
$ \displaystyle { {AF \over FB}\cdot {BD \over DC}\cdot {CE \over EA}=1 } $
上記がチェバの定理なんですが、この定理のポイントはズバリ、辺の比を掛け合わせたものは1に等しくなる、と言う点です。まぁ方程式をそのまま文章にしただけですが、ちょっと感動していますのでお許し下さい。( ^^;
よくもまぁ辺の比を掛け合わせたらどうなるか? …なんて考えたものです。
これを証明するのはそれほど難しくはありません。3角形の面積の求め方と、同じ比分量の値を引いた残りの部分もまた等しくなる、と分かっていれば理解できます。

上図で、(1) のグリーンとピンクの面積比、分かりますよね? 辺 $ FO $ を3角形の高さと見ると、面積比は底辺のそれぞれの辺 $ AF,~FB $ の長さの比と同じになることがわかるでしょう。
それが分れば (2) も同様にグリーンとピンクの面積比はそれぞれの辺 $ AF,~FB $ の長さの比と同じことが分かります。
この (2) の3角形から (1) の3角形を引いて残った部分の面積比、つまり (3) のグリーンとピンクの面積比も分かりますよね?
辺 $ AF,~FB $ の長さの比と同じです。

上図で、(1) のグリーンとピンクの面積比、分かりますよね? 辺 $ FO $ を3角形の高さと見ると、面積比は底辺のそれぞれの辺 $ AF,~FB $ の長さの比と同じになることがわかるでしょう。
それが分れば (2) も同様にグリーンとピンクの面積比はそれぞれの辺 $ AF,~FB $ の長さの比と同じことが分かります。
この (2) の3角形から (1) の3角形を引いて残った部分の面積比、つまり (3) のグリーンとピンクの面積比も分かりますよね?
辺 $ AF,~FB $ の長さの比と同じです。
上図は Wikipedia に載っている証明の一部分
$ {\displaystyle {AF \over FB}={\triangle AFC-\triangle AFO \over \triangle BFC-\triangle BFO}={\triangle AOC \over \triangle BOC}.} $
を図示化したものですが、同様に残りの2つも説明できますので、下記の2つが成り立つのは直ぐにお分かりになると思います。
$ {\displaystyle {BD \over DC}={\triangle BDA-\triangle BDO \over \triangle CDA-\triangle CDO}={\triangle BOA \over \triangle COA}.} $
$ {\displaystyle {CE \over EA}={\triangle CEB-\triangle CEO \over \triangle AEB-\triangle AEO}={\triangle COB \over \triangle AOB}.} $
さて、ここからがチェバの定理の面白いところです。3つの辺の比を掛け合わせるといったいどんな値になるのか?
$ \displaystyle { {AF \over FB}\cdot {BD \over DC}\cdot {CE \over EA}=? } $
これが、下記の式と同等なのは既に見て来ました。
$ \displaystyle { {AF \over FB}\cdot {BD \over DC}\cdot {CE \over EA}=? } $
これが、下記の式と同等なのは既に見て来ました。
$ {\displaystyle {\triangle AOC \over \triangle BOC}\cdot {\triangle BOA \over \triangle COA}\cdot {\triangle COB \over \triangle AOB}} $
一見すると、どうしてこれが1になるのか分かり難いのですが、下記のように書き換えると見えて来ます。
$ {\displaystyle {\triangle AOC \over \triangle BOC}\cdot {\triangle BOA \over \triangle AOC}\cdot {\triangle BOC \over \triangle BOA}} $
3角形を表す表記が分母と分子で同じにしないとね。Wikipedia に載っている証明式では分かり難いです。
分数の掛け算が約分出来る!、と分かり易いようにアルファベットを同じ順番で書いて3角形を示すべきですよね。
分数の掛け算が約分出来る!、と分かり易いようにアルファベットを同じ順番で書いて3角形を示すべきですよね。
では今日も1日の習慣を始めます。小さな一歩・挑戦を試みます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 習慣作りのための、小さな課題 | ☆ 実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿後 |
加減算 21~120の足し算1回、21~120の引き算1回 乗算 せず |
| 2階に上り降り時、懸垂1回 (ボルダリングの体力獲得) ブログ投稿後 |
グリップ40回、腕立て20回、腹筋20回、完全懸垂1回 |
| 数学の問題 1問 (物理学の数式の理解力の獲得) 90分 |
チャート式 数学 白II+B:せず チャート式 数学 青I+A:p419 実用数学技能検定 要点整理 2級:せず 数学の答え合わせは後でまとめてやる:機会なし 数学の学習に取り組んだ時間:57分 |
| 規則正しい生活 基本習慣 |
昨日・寝床に入った時間:午前00時04分 今朝・6時台に布団から出る:06時28分 朝 --- ブログの投稿 --- |
閲覧(9367)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



