時空 解 さんの日記
2019
9月
16
(月)
09:04
本文
皆さん、おはようございます。時空 解です。
数学検定のテキスト、実用数学技能検定 要点整理 2級 を学習していてハマった問題がありました。
p71 の 応用問題1
$ \triangle ABC $ について、$ AB = 3 $ , $ AC = 5 $ , $ \angle A = 120^\circ $ のとき、$ \angle A $ の二等分線と辺 $ BC $ の交点を $ D $ として、次の問いに答えなさい。
(1) 線分 $ AD $ の長さを求めなさい。
(2) 線分 $ BD $ の長さを求めなさい。
この問題の (1) は3角形の面積 $ \triangle ABC = \triangle ABD + \triangle ACD $ を利用すれば解けます。
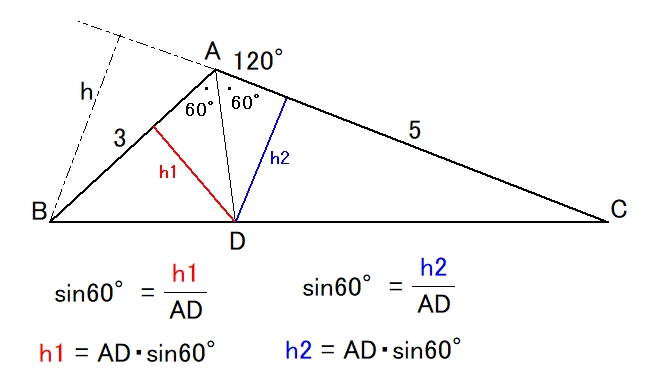
全体の3角形 $ \triangle ABC $ の高さ $ h $ は $ h = 3 \cdot \sin 120^\circ $ ですよね。ですから底辺が $ 5 $ ですから面積は求まります。
$ \triangle ABD $ と $ \triangle ACD $ も同じように面積を求める式を立てて、$ AD $ に付いて $ \triangle ABC = \triangle ABD + \triangle ACD $ を解けばよいです。
でもこの問題って、3角形の面積ではなくて線分の合計でも解けると考えたりもしませんか?
$ BC = BD + DC $ ですよね。
ですから、余弦定理でそれぞれ $ BC $ と $ BD $、$ DC $ の線分を求める式を書いてやって、$ AD $ を解いてやればいいと想ったのですが…。
$ BC = BD + DC $ ですよね。
ですから、余弦定理でそれぞれ $ BC $ と $ BD $、$ DC $ の線分を求める式を書いてやって、$ AD $ を解いてやればいいと想ったのですが…。
ハマりました。どうしてもこの計算だと正しい答えが出て来ません。
間違いに気が付くのに時間が掛かりました。
皆さんは直ぐに分かったと思いますが、余弦定理を使うと線分の長さは2乗なんですよね。ですから私は
$ BC^2 = BD^2 + DC^2 $
をやっていた事になります。
$ a^2 + b^2 $ と $ (a + b)^2 $ は同じではありません。
これになかなか気が付きませんでした。
初めに3角形の線分の合計を考えていたので、つい余弦定理に出てくる線分の長さは2乗の値であることを見落としていたんです。
皆さんは直ぐに分かったと思いますが、余弦定理を使うと線分の長さは2乗なんですよね。ですから私は
$ BC^2 = BD^2 + DC^2 $
をやっていた事になります。
$ a^2 + b^2 $ と $ (a + b)^2 $ は同じではありません。
これになかなか気が付きませんでした。
初めに3角形の線分の合計を考えていたので、つい余弦定理に出てくる線分の長さは2乗の値であることを見落としていたんです。
$ a^2 + b^2 $ と $ (a + b)^2 $ が等しいなんて、因数分解の問題を解いている時なら想わないんですけどね。
これが3角形の線分に置き換わると分からないなんて…自分自身の思い込みに衝撃です!
みなさんはこんな勘違い、しませんか? …うーむ…しませんか…。
これが3角形の線分に置き換わると分からないなんて…自分自身の思い込みに衝撃です!
みなさんはこんな勘違い、しませんか? …うーむ…しませんか…。
では今日も1日の習慣を始めます。小さな一歩・挑戦を試みます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 習慣作りのための、小さな課題 | ☆ 実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿後 |
加減算 出来ず 乗算 せず |
| 2階に上り降り時、懸垂1回 (ボルダリングの体力獲得) ブログ投稿後 |
できず |
| 数学の問題 1問 (物理学の数式の理解力の獲得) 90分 |
チャート式 数学 白II+B:せず チャート式 数学 青I+A:p425,p426 実用数学技能検定 要点整理 2級:p69 ~ p71 数学の答え合わせは後でまとめてやる:〇 数学の学習に取り組んだ時間:67分 |
| 規則正しい生活 基本習慣 |
昨日・寝床に入った時間:23時50分 今朝・6時台に布団から出る:06時40分 朝 --- ブログの投稿 --- |
閲覧(7892)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



