50代から理数を学ぶ - こんな簡単な問題がピンとこないなんて…円に内接する４角形は、１つの内角が、その対角の外角に等しい

Home > ブログ > 時空解 > 数学 > こんな簡単な問題がピンとこないなんて…円に内接する４角形は、１つの内角が、その対角の外角に等しい

時空解さんの日記

2019

9月 22

(日)

09:28

こんな簡単な問題がピンとこないなんて…円に内接する４角形は、１つの内角が、その対角の外角に等しい

前の日記次の日記

カテゴリー数学

本文

皆さん、おはようございます。時空解です。

昨日、かなり時間を掛けて考えたのに分からないかった問題がありました。
それで答えを見てみると…。

なんだ！　

　直ぐに分からないといけないような問題でした。
ちょっとショックです。

問題は下記のとおり。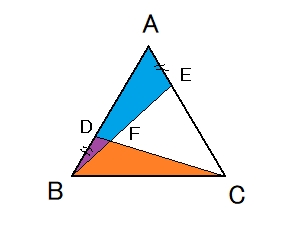

青チャート「改訂版チャート式基礎からの数学I+A」p433 練習８３

右の図の正３角形 ABC で、辺 AB, AC 上にそれぞれ点 D (点 A, B とは異なる) 、E (点 A, C とは異なる) をとり、BD = AE となるようにする。
BE と CD の交点を F とするとき、４点 A, D, F, E が１つの円周上にあることを証明せよ。

この問題を解くためには、２つの知識が必要です。

３角形の合同条件
・２辺とその間の角が等しい

４角形の内接円の定理
・１つの内角が、その対角の外角に等しい

この２つです。ちゃんとこの２つは知っていたのですけどね。合同である３角形が目に入らなかったのです。

３角形ABE ≡ ３角形BCD

ですよね。
これで角AEB = 角BDC が成立しますので、４角形ADFE は１つの内角が、その対角の外角に等しいことが言えました。

私は円に内接する４角形のもう一つの定理
「１組の対角の和が、180° である」
を利用して問題を証明しようと考えてしまいました。そうすると３角形が合同であることが目に入りません…

いちど考え方の方向性を決めてしまうとなかなかね。

では今日も１日の習慣を始めます。小さな一歩・挑戦を試みます。

応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは１日にして成らず、です。

(ポチッとブログ村のバナーをクリックしてね）

「休日の使い方」の実施状況
★ 平日を充実させるために…	☆ 実施状況
数学の問題１問 (物理学の数式の理解力の獲得) ランチ前	チャート式数学白II+B：せずチャート式数学青I+A： p433 実用数学技能検定要点整理２級：p84～p93 スタディサプリ：せず数学の答え合わせは後でまとめてやる：〇数学の学習に取り組んだ時間：1時間46分
２階に上り降り時、懸垂１回 (ボルダリングの体力獲得) ランチ & 買い物前	グリップ４０回、腕立て２０回、腹筋２０回、懸垂２回
コンテンツ１つ、小説１節ランチ & 買い物後	コンテンツできず小説１節できず
そろばんの練習５問 (暗算の獲得) 夜、寝る前	加減算２１～１２０の足し算２回掛け算せず
規則正しい休日の生活基本習慣	昨日・寝床に入った時間：午前００時０３分今朝・７時に布団から出る：０６時３０分朝 --- ブログの投稿 ---

閲覧(4501)

コメントを書く
コメントを書くにはログインが必要です。