50代から理数を学ぶ - 不等式と絶対値記号、やっと理解できて来た。

Home > ブログ > 時空解 > 数学 > 不等式と絶対値記号、やっと理解できて来た。

時空解さんの日記

2015

11月 23

(月)

10:55

不等式と絶対値記号、やっと理解できて来た。

前の日記次の日記

カテゴリー数学

本文

みなさん、こんにち。
「改訂版チャート式解法と演習数学Ⅰ+Aー数研出版」を始めから順次勉強をして行く事で、やっと絶対値記号が含まれる不等式を正しく理解する事が出来るようになりました。学生時代ならば「これが正しい解答なのですよ」と先生に言われても私は「ウソだ！」と心の中で思って、信用しなかった事でしょう。しかし、「改訂版チャート式解法と演習数学Ⅰ+Aー数研出版」を始めから丁寧に勉強して行く事で、信用する事ができるようになってきました。
ちょっと一つの問題を例にとってみてみましょう。問題は「改訂版チャート式解法と演習数学Ⅰ+Aー数研出版」５２ページの一番最後の問題です。

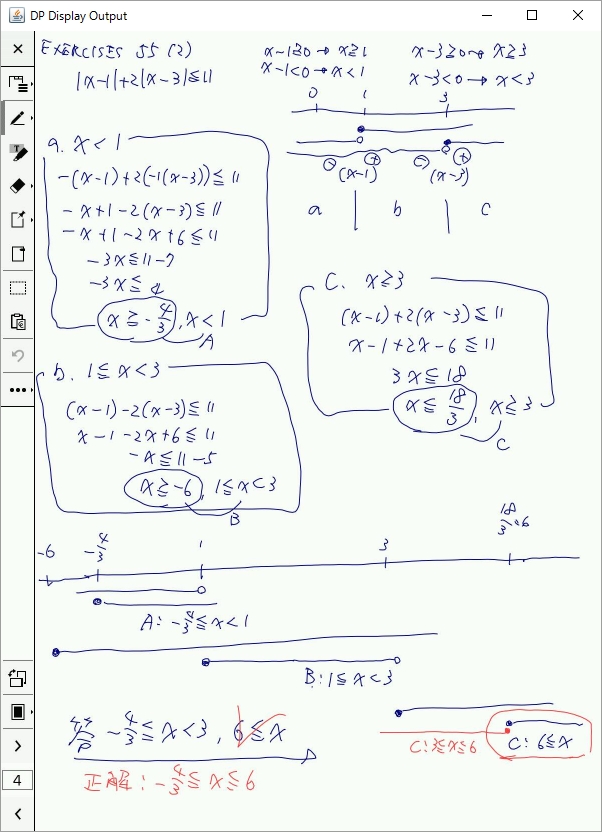
考え方としては、初めに絶対値記号の中の符号の場合分けをします。上図では a,b,c と言う三つの領域に分けています。
次に絶対値記号を外すために場合分けされた領域ごとに、与式を変形します。上図では、a. X＜1 、b. 1≦X＜3 、c. X≧3 の３つの領域について与式を変形しています。
最後に a.b.c それぞれの領域における X の範囲 A,B,C を求めて、答えを出しています。
図では、C の X の範囲がケアレスミスしています。私のウッカリです。

ともかく、下記の手順を踏まえないと与式から解答にたどり着くことはできません。
① 場合分け
② 場合分けに応じた絶対値記号の取り外し ( 変数 X の取りうる値を ± から + のみにする )
③ 場合分けの X の範囲と与式の変形から得た X の結果から、同時に満たす X の範囲を求める ( 論理的には and する )
④ 場合分けそのぞれの X の範囲を合わせる ( 論理的には or する )

「改訂版チャート式解法と演習数学Ⅰ+Aー数研出版」を始めからキチンと学ばないと、
・絶対値記号を外すためにどうして場合分けするのか？
・ X の範囲を考える時に、同時に満たす X 範囲(and)、合わせた範囲(or)、その使い分けを、どう考えるの？
上記２つが壁となって、理解できないはずです。現役の学生でも教えてもらったりすると「どうしてかなぁ」と思ったりするはずです。そんな時先生はよくこんな事を言うものです。
「ようするに慣れですね、数式に慣れてください」
なんてね。これでは答えになっていません。

「適当な事を言っていやがるな・・・」

と、先生をかんぐりたくなります。

しかし私もみなさんに問われたら、きっと先生と同じ事をいうでしょう。( ^^;

それほど微妙な点です。やはりコツコツと参考書を始めから順次、理解して行くしかありません。こうしてみると「改訂版チャート式解法と演習数学Ⅰ+Aー数研出版」と言う書籍はキチンとした考えのもと編集されている、優れた参考書であると感じる次第です。
では今日はこの辺で。

閲覧(10301)

コメントを書く
コメントを書くにはログインが必要です。