時空 解 さんの日記
2019
11月
21
(木)
09:27
本文
皆さん、おはようございます。時空 解です。
今日の朝も寒いですね。皆さんはどうお過ごしですか?
私は昨日の朝、ガスファンヒーターを押し入れから出したところです。そのおかげで快適にブログを書いています。
私は昨日の朝、ガスファンヒーターを押し入れから出したところです。そのおかげで快適にブログを書いています。
上記の論文について書いてみます。
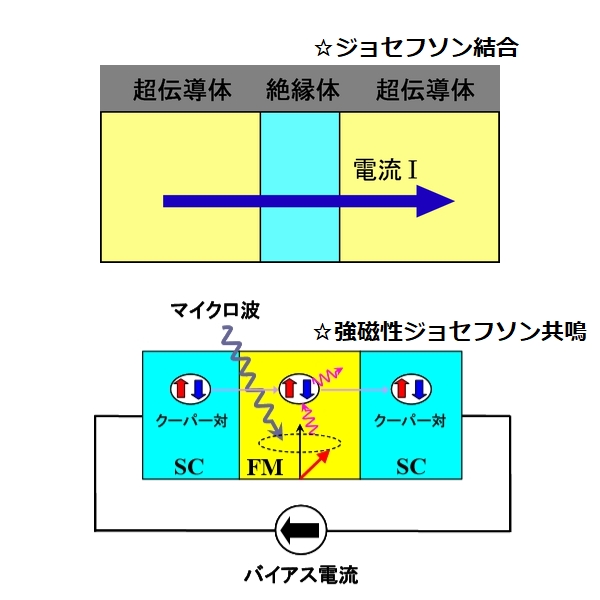
この論文は題名のとおり「強磁性ジョセフソン共鳴」という現象を提案しているものです。結論を論文内の文章から引用すると下記のようになります。
本研究の結果は、SC/FM/SC 接合が、スピン波を観測する新しい実験法や交流-直流超伝 導コンバータ(超伝導電流の整流作用)に用いられる素子となりうることを示唆している。 本研究で展開された「強磁性ジョセフソン共鳴」の理論は、今後の SC/FM/SC 接合における 動的な性質の研究の基礎になり、量子ビットの開発にも新たな指針を与えるものと大いに 期待される。
実のところ、量子コンピュータで利用されている量子ビット素子は、まだジョセフソン接合によるジャンクションのようですが、今後は「強磁性ジョセフソン共鳴 (SC/FM/SC接合)」を利用した素子によるジャンクションへと、取って変わるのかも知れませんね。
ところで…
電流が流れるためには電位差が必要だ! …と言う常識が私にはありましたが、皆さんは如何てしょうか?
「電位差のないところでは電流は流れない」
なんて思っていたんです。
でも今回の論文を読んで、この常識が間違っていたのが分かりました。
「強磁性ジョセフソン共鳴」である SC/FM/SC接合 はマイクロ波を照射することで交流電流であったり直流電流が流れたりと、コントロールさえもできるんですね。この点が今回の論文の趣旨ですが、それ以前に、ジョセフソン結合を流れる電流が私に取っては衝撃でした。そこの部分をWikipedia の "ジョセフソン効果:原理" より引用してみましょう。
電流が流れるためには電位差が必要だ! …と言う常識が私にはありましたが、皆さんは如何てしょうか?
「電位差のないところでは電流は流れない」
なんて思っていたんです。

でも今回の論文を読んで、この常識が間違っていたのが分かりました。
「強磁性ジョセフソン共鳴」である SC/FM/SC接合 はマイクロ波を照射することで交流電流であったり直流電流が流れたりと、コントロールさえもできるんですね。この点が今回の論文の趣旨ですが、それ以前に、ジョセフソン結合を流れる電流が私に取っては衝撃でした。そこの部分をWikipedia の "ジョセフソン効果:原理" より引用してみましょう。
超伝導状態の物質はその内部で、すべてのクーパー対がボースアインシュタイン凝縮により全体として1つの巨大な電子対としてふるまう。つまり、このとき超伝導を示す電子の物質波の位相は巨大量子化によって物質の隅々まで全く同じ状態になる。ミクロでしか作用しなかった量子効果が、超伝導によってマクロな巨大量子状態になって現れたことになる。
仮に2つの超伝導物質を、最初は離したままで常伝導から超伝導へと変えてやると、これらの内部にも完全に位相のそろった大きな電子対をそれぞれ抱えた大きな塊が2つ出来上がる。これら2つの塊は物質波の位相が不揃いであり、近づければ位相を揃えた1つの塊になろうと位相差分の電流が片方からもう一方へと流れる。このとき電位差は存在しないのに、電流だけが流れる。これがジョセフソン電流である。
ジョセフソン効果:原理より引用
ジョセフソンは、こんな現象が起こることを大学院生であったとき、演習問題を解く過程で計算式までも導き出したなんて、本当にびっくりです。
この計算式のもととなっているのはどうやらシュレディンガー方程式のようです。
この計算式のもととなっているのはどうやらシュレディンガー方程式のようです。
やっぱりシュレディンガー方程式と言うのは、量子力学に取ってとても大切な方程式なんですね。改めてそう思いました。
ちなみに "「ファインマン物理学」を読む" と言うブルーバックス書もあるのですが、その中にも「4.シュレディンガー方程式の登場」と言う章があります。注目すべき方程式なのでしょう。
ちなみに "「ファインマン物理学」を読む" と言うブルーバックス書もあるのですが、その中にも「4.シュレディンガー方程式の登場」と言う章があります。注目すべき方程式なのでしょう。
ファインマン物理学…学生のころから本棚に飾ってあるんですけどね…若い頃に読んでおけばねぇ…。
では今日も休日を始めます。休日の充実こそ、人生の充実です。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
![]()
| ★ 平日を充実させるために… | ☆ 実施状況 |
|---|---|
| 2階に上り降り時、懸垂1回 (ボルダリングの体力獲得) ランチ & 買い物前 |
できず |
| 数学の問題 1問 (物理学の数式の理解力の獲得) ランチ & 買い物の前後 |
チャート式 数学 青I:せず チャート式 数学 青A:せず チャート式 数学 青II:せず チャート式 数学 青B:せず 実用数学技能検定 要点整理2級:過去問の見直し (6問 ) 実用数学技能検定 要点整理準1級:せず 数学の学習に取り組んだ時間:1時間07分 チャート式 新物理 物理基礎・物理:せず ゼロからの大学物理 熱力学と統計力学:せず 物理学の学習に取り組んだ時間:0時間00分 |
| そろばんの練習5問 (暗算の獲得) 夜、寝る前 |
加減算 できず 掛け算 せず |
| 規則正しい休日の生活 基本習慣 |
昨日・寝床に入った時間:23時38分 今朝・6時台に布団から出る:06時58分 朝 --- ブログの投稿 --- |
閲覧(17594)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記