50代から理数を学ぶ - 1 から 2007 までの整数をすべてかけたとき、0 は一の位から続けていくつ並びますか。 → １０進数と８進数の素因数

Home > ブログ > 時空解 > 数学 > 1 から 2007 までの整数をすべてかけたとき、0 は一の位から続けていくつ並びますか。 → １０進数と８進数の素因数

時空解さんの日記

2019

12月 9

(月)

12:04

1 から 2007 までの整数をすべてかけたとき、0 は一の位から続けていくつ並びますか。 → １０進数と８進数の素因数

前の日記次の日記

カテゴリー数学

本文

皆さん、おはようございます。( と言うよりも、もうお昼になってしまいましたが… ) 時空解です。

今日も表題にあるように、
・1 から 2007 までの整数をすべてかけたとき、0 は一の位から続けていくつ並びますか。
と言う問題に関連することを書いてみます。

・駒場東邦中学校　2007年2月1日過去問
　　算数 mat.pdf　問２

昨日は $ 345 \times 346 = 2 \times 3 \times 5 \times 23 \times 173 $ を例にして「素因数に分解」することの意味を少し説明致しました。素因数分解をして $ 345 \times 346 $ の中に $ 2 \times 5 $ を見つければ、それが一の位に０を作って行くことをイメージして貰えたと想います。

今日は $ 1 $ から $ 10 $ までの数量の掛け算を使って、１０進数、８進数の２つを比較し、０の付き方の違いを見てみましょう。
そうすることで、より素因数分解の意味と、一の位に０が付く仕組みが見えて来ると想います。

まずは 1 から 10 の整数を全て掛け合わせてみましょう。

$ 1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9 \times 10 = 3628800 $

となります。
これを素因数分解した形で書くと

$ 1 \times 2 \times 3 \times (2 \times 2) \times 5 \times (2 \times 3) \times 7 \times (2^3) \times (3^2) \times (2 \times 5) = 3628800 $

となります。

ではこれを８進数でやってみます。

$ 1_8 \times 2_8 \times 3_8 \times 4_8 \times 5_8 \times 6_8 \times 7_8 \times 10_8 \times 11_8 \times 12_8 = 15657400_8 $

ですね？
これを素因数分解した形で書くと

$ 1_8 \times 2_8 \times 3_8 \times ({2_8}^2) \times 5_8 \times (2_8 \times 3_8) \times 7_8 \times ({2_8}^3) \times ({3_8}^2) \times (2_8 \times 5_8) = 15657400_8 $

となります。

ポイントは１０進数の８のところからですね。
１０進数の $ 8 $ は８進数で表記すると $ 10_8 $ 。9 は $ 11_8 $ 。10 は $ 12_8 $ です。
$ 10_8,~11_8,~12_8 $ を素因数に分解すると本当に $ ({2_8}^3),~({3_8}^2),~(2_8 \times 5_8) $ になるんでしょうか？

これは慣れないとちょっと戸惑ったり、答えが分っても少し自信が持てなかったりします。

こんな時にこそ、ネット上にある計算知能 Wolfram Alpha を利用してみましょう。
下記にリンクを通しておきましたので、サイトを開いて確認してみて下さいね。

・Wolfram Alpha 計算知能

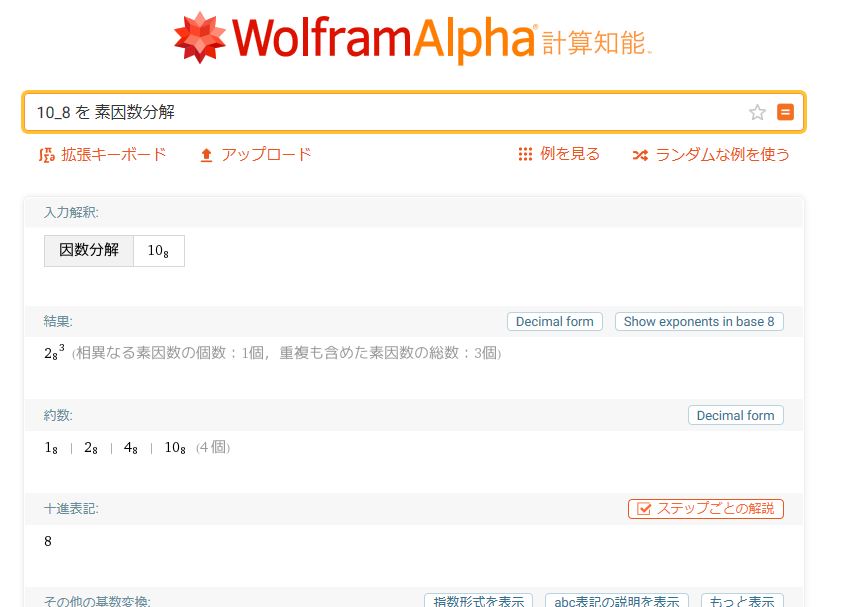
サイトを開くと、オレンジ枠内に「計算したいことや知りたいことを入力してください.」と表示されているのが分ると想います。
このオレンジ枠内に、下記の文字列をコピペして、右端にある "＝" アイコンをクリックしてみてください。

10_8 を素因数分解

下記のようにちゃんと表示されたでしょうか？

さて、ここまでの解説で、８進数のときの０の付き方、ピン！と来ましたでしょうか？

まずは１０進数の 1 から 10 までの整数全てを掛けたら、１の位から０がいくつ並ぶのかを見てみましょう。

$ 1 \times 2 \times 3 \times (2 \times 2) \times 5 \times (2 \times 3) \times 7 \times (2^3) \times (3^3) \times (2 \times 5) = 3628800 $

上式をみると分かるとおり、$ 2 $ の個数は８個で $ 5 $ の個数は２個ありますよね。
これが $ 3628800 $ と言う数字の下２桁に０が２つ並んでいる理由です。$ 2 $ と $ 5 $ の組み合わせ (掛け合わせ) のみが $ 10 $ を作りますから、 $ 5 $ の個数に依存します。

下２桁に０を２つ並べるには、$ 2 $ が２個、$ 5 $ が２個で可能です。ですから $ 2 $ は８個もいりません。では余った６個はどう振る舞うでしょうか？
ご自分で素因数として $ 5 $ を含まない任意の数を選んで $ 2^6 $ を掛けてみて下さい。もう下の桁に０が増えることはありません。ですから余った６個の $ 2 $ は気にしなくても大丈夫です。

次は８進数に付いて、です。

$ 1_8 \times 2_8 \times 3_8 \times ({2_8}^2) \times 5_8 \times (2_8 \times 3_8) \times 7_8 \times ({2_8}^3) \times ({3_8}^2) \times (2_8 \times 5_8) = 15657400_8 $

上式をみて、１の位に０を付けるのは何か、見て取れるのではないでしょうか？

$ 2_8 $ が３個で１の位に０が１つ付く

と言うことが分ると想います。
$ 2_8 $ の数を数えると８個ですよね。従って $ (2_8)^3 $ ２つと $ 2_8 $ ２個です。ですから０は２つ付そうですよね。

確かに $ 15657400_8 $ には下の桁に２つ０が付いています。
これに $ 2_8 $ を掛けてみましょう。
これは余っている $ 2_8 $ ２個に $ 2_8 $ をもう一つ追加すると言う意味合いです。

$ 15657400_8 \times 2_8 = 33537000_8 $

確かに０が３つに増えましたね。
これを確認するには先ほどの Wolfram Alpha 計算知能に下記の文字列をコピペして＝をクリックしてみて下さいね。

15657400_8 * 2_8

つまり、余った $ 2_8 $ ２個にもう一つ $ 2_8 $ を追加すると $ {2_8}^3 $ になり、８進数では一の位に０が一つ増えることになるんです。

では今日はここまでにしておきます。
明日はちゃんと表題に示してある問題に向き合いますよ。

では今日も休日を始めます。休日の充実こそ、人生の充実です。

応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは１日にして成らず、です。

(ポチッとブログ村のバナーをクリックしてね）

「小さな習慣 ( 良い習慣化計画 ) 」の実施状況
★ 習慣作りのための、小さな課題	☆ 実施状況
そろばんの練習５問 (暗算の獲得) ブログ投稿後	加減算１1～１１０の足し算１回、引き算１回乗算せず
２階に上り降り時、懸垂１回 (ボルダリングの体力獲得) ブログ投稿後	グリップ４０回、腕立て２０回、腹筋２０回、完全懸垂１回
数学の問題１問 (物理学の数式の理解力の獲得) ９０分	チャート式数学青I：できずチャート式数学青Ａ：できずチャート式数学青II：できずチャート式数学青Ｂ：できず実用数学技能検定要点整理２級：せず実用数学技能検定要点整理準１級：せず数学の答え合わせは後でまとめてやる：機会なし数学の学習に取り組んだ時間：0時間00分
規則正しい生活基本習慣	昨日・寝床に入った時間：２３時５０分今朝・６時台に布団から出る：０７時００分朝 --- ブログの投稿 ---

閲覧(5703)

コメントを書く
コメントを書くにはログインが必要です。