時空 解 さんの日記
2019
12月
10
(火)
09:45
本文
皆さん、おはようございます。時空 解です。
今日も表題にもあるように、
・1 から 2007 までの整数をすべてかけたとき、0 は一の位から続けていくつ並びますか。
と言う問題に関連することを書いてみます。
・1 から 2007 までの整数をすべてかけたとき、0 は一の位から続けていくつ並びますか。
と言う問題に関連することを書いてみます。
昨日は 1 から 10 の整数を10進数表記と8進数表記のときの違いを見てみました。
ちょっと遠回りだったかも知れませんが ( すみません… (^^; ) 「1の位に0が付く」と言う桁上げと素因数の関係が見えたのではないでしょうか?
8進数のときの「1の位に0が付く」と言う桁上げは、$ 1_8 $ から $ 12_8 $ に含まれている全ての素因数の中の $ 2_8 $ の個数で決まりましたね。
$ 2_8 $ が3つ集まるごとに0が付きます。
10進数のときの「1の位に0が付く」と言う桁上げは、$ 1 $ から $ 10 $ に含まれる全ての素因数の中の $ 2 $ と $ 5 $ の個数、特に $ 5 $ の個数に依存しています。
今日はそれを確かめてみましょう。
ちょっと遠回りだったかも知れませんが ( すみません… (^^; ) 「1の位に0が付く」と言う桁上げと素因数の関係が見えたのではないでしょうか?
8進数のときの「1の位に0が付く」と言う桁上げは、$ 1_8 $ から $ 12_8 $ に含まれている全ての素因数の中の $ 2_8 $ の個数で決まりましたね。
$ 2_8 $ が3つ集まるごとに0が付きます。
10進数のときの「1の位に0が付く」と言う桁上げは、$ 1 $ から $ 10 $ に含まれる全ての素因数の中の $ 2 $ と $ 5 $ の個数、特に $ 5 $ の個数に依存しています。
今日はそれを確かめてみましょう。
では、これから $ 2 $ の個数と $ 5 $ の個数を数え上げてみます。
1 から 2007 までの整数に対してこれをやるのは現実的ではありませんので、まずは 1 から 33 までの整数でやってみました。
1 から 2007 までの整数に対してこれをやるのは現実的ではありませんので、まずは 1 から 33 までの整数でやってみました。

上に示した "1 から 33 までの整数の素因数分解 表" をみて頂くとイメージが沸き易いと想います。
まずは $ 2 $ の個数からやってみましょう。
$ 1 $ から $ 33 $ までの整数の中に素因数の $ 2 $ がいくつ含まれているかを調べる場合。
まずは $ 2 $ の倍数である整数の数を調べれば良いことは分かりますよね?
$ 1 $ から $ 33 $ までの整数の中に素因数の $ 2 $ がいくつ含まれているかを調べる場合。
まずは $ 2 $ の倍数である整数の数を調べれば良いことは分かりますよね?
$ 2 $, $ 4 $, $ 6 $, $ 8 $, $ 10 $, $ 12 $, $ 14 $, $ 16 $, $ 18 $, $ 20 $, $ 22 $, $ 24 $, $ 26 $, $ 28 $, $ 30 $, $ 32 $ です。
でも、4 の中にはもう一つ $ 2 $ が含まれています。8 の中にも、あと2つ含まれていますよね。
$ 2 $ の個数は重複なく、漏れなく数え上げなくてはいけません。
これを頭の中でやろうとすると、重複しているのかいないのか?漏れはないのかがちょっと不安です。
ですから一度は "1 から 33 までの整数の素因数分解 表" を作ってみるのが不安を解消する近道でしょう。そうすると、下に示すように、黄色い部分を順に調べて行くことが、重複なく漏れなく数え上げる方法だと分ると想います。
$ 2 $ の個数は重複なく、漏れなく数え上げなくてはいけません。
これを頭の中でやろうとすると、重複しているのかいないのか?漏れはないのかがちょっと不安です。
ですから一度は "1 から 33 までの整数の素因数分解 表" を作ってみるのが不安を解消する近道でしょう。そうすると、下に示すように、黄色い部分を順に調べて行くことが、重複なく漏れなく数え上げる方法だと分ると想います。
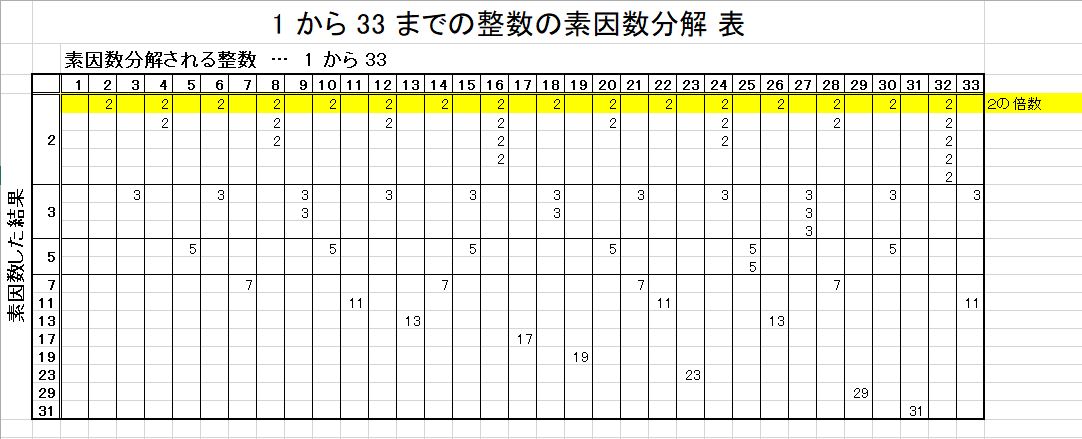




$ 2 $ についてはこれで数え上げられると想います。
まとめると
$ 33 $ は $ 2^5 $ よりも大きく $ 2^6 $ よりも小さいので、1 から 33 までの整数の中の素因数 $ 2 $ を数えるには
$ 2 $ の倍数の整数、 $ 2^2 $ の倍数の整数、 $ 2^3 $ の倍数の整数、 $ 2^4 $ の倍数の整数、 $ 2^5 $ の倍数の整数、それぞれの個数を数えればよい。
$ 33 $ は $ 2^5 $ よりも大きく $ 2^6 $ よりも小さいので、1 から 33 までの整数の中の素因数 $ 2 $ を数えるには
$ 2 $ の倍数の整数、 $ 2^2 $ の倍数の整数、 $ 2^3 $ の倍数の整数、 $ 2^4 $ の倍数の整数、 $ 2^5 $ の倍数の整数、それぞれの個数を数えればよい。
$ 5 $ についても同じです。
$ 33 $ は $ 5^2 $ よりも大きく $ 5^3 $ よりも小さいので、1 から 33 までの整数の中の素因数 $ 5 $ を数えるには
$ 5 $ の倍数の整数、 $ 5^2 $ の倍数の整数、それぞれの個数を数えればよい。
$ 33 $ は $ 5^2 $ よりも大きく $ 5^3 $ よりも小さいので、1 から 33 までの整数の中の素因数 $ 5 $ を数えるには
$ 5 $ の倍数の整数、 $ 5^2 $ の倍数の整数、それぞれの個数を数えればよい。
あとは素因数 $ 2 $ と $ 5 $ の一組 $ 2 \times 5 = 10 $ なので、 $ 2 \times 5 $ の組の個数がすなわち1の位にから並ぶ0の数になります。
これと同じことを "1 から 2007 までの整数をすべてかけたとき" に付いてもやってみれば、いよいよ答えがでます。
まず $ 2007 $ は
$ 2^10 \leqq 2007 \leqq 2^11 $
$ 5^4 \leqq 2007 \leqq 5^5 $
まず $ 2007 $ は
$ 2^10 \leqq 2007 \leqq 2^11 $
$ 5^4 \leqq 2007 \leqq 5^5 $
です。
ここで $ 2 $ の素因数の個数は $ 5 $ の素因数の個数よりも明らかに多いので、$ 5 $ の素因数の個数のみを調べればよい。
ここで $ 2 $ の素因数の個数は $ 5 $ の素因数の個数よりも明らかに多いので、$ 5 $ の素因数の個数のみを調べればよい。
1 から 2007 までの整数の内、$ 5 $ の倍数の整数の数は $ 2007 \div 5 = 401 $ 余り $ 2 $
1 から 2007 までの整数の内、$ 5^2 $ の倍数の整数の数は $ 2007 \div 5^2 = 80 $ 余り $ 7 $
1 から 2007 までの整数の内、$ 5^3 $ の倍数の整数の数は $ 2007 \div 5^3 = 16 $ 余り $ 7 $
1 から 2007 までの整数の内、$ 5^4 $ の倍数の整数の数は $ 2007 \div 5^4 = 3 $ 余り $ 132 $
1 から 2007 までの整数の内、$ 5^2 $ の倍数の整数の数は $ 2007 \div 5^2 = 80 $ 余り $ 7 $
1 から 2007 までの整数の内、$ 5^3 $ の倍数の整数の数は $ 2007 \div 5^3 = 16 $ 余り $ 7 $
1 から 2007 までの整数の内、$ 5^4 $ の倍数の整数の数は $ 2007 \div 5^4 = 3 $ 余り $ 132 $
$ 401 + 80 + 16 + 3 = 500 $
これで答が出ました。
問:1 から 2007 までの整数をすべてかけたとき、0 は一の位から続けていくつ並びますか。
答:$ 500 $ 個続けて並ぶ
答:$ 500 $ 個続けて並ぶ
では今日も1日の習慣を始めます。小さな一歩・挑戦を試みます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 習慣作りのための、小さな課題 | ☆ 実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿後 |
加減算 できず 乗算 せず |
| 2階に上り降り時、懸垂1回 (ボルダリングの体力獲得) ブログ投稿後 |
できず |
| 数学の問題 1問 (物理学の数式の理解力の獲得) 90分 |
チャート式 数学 青I:できず チャート式 数学 青A:できず チャート式 数学 青II:p13 チャート式 数学 青B:できず 実用数学技能検定 要点整理 2級:せず 実用数学技能検定 要点整理 準1級:せず 数学の答え合わせは後でまとめてやる:〇 数学の学習に取り組んだ時間:1時間27分 |
| 規則正しい生活 基本習慣 |
昨日・寝床に入った時間:23時40分 今朝・6時台に布団から出る:06時30分 朝 --- ブログの投稿 --- |
閲覧(10565)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



