時空 解 さんの日記
 前の日記
次の日記
前の日記
次の日記 カテゴリー
マスペディア 1000
カテゴリー
マスペディア 1000
トピックの第239番目から248番目までは、正直どうでもいいような立体の分類が示されます。
興味が湧きません。
立体図形を分類するには、立体を作っている面の形とか、頂点の数、各辺の長さの関係とかで分類をするのですが、そんな分類がいったい何の役に立つのか…トポロジーと言う言葉は知っていますが、それとは違うようですね。
立体の分類について、有名な先人が存在しているようです。
日本語版の Wikipedia には彼の名前のページは載っていませんが、「シュレーフリ記号」と言うものが有って、その説明は載っています。
この記号は正多胞体を
{p,q,r,...}
の形で立体を表すもののようです。
"正多胞体" と言う単語は英語の発音では "ポリトープ" と言うようですね。
さっそくその立体がどんなものかを調べてみると…
チンプンカンプンです。
調べてみると、一言でいうと3次元に存在している立体を4次元、5次元…に拡張することのようですね。
これは超立体の表記にも使用されるようです。
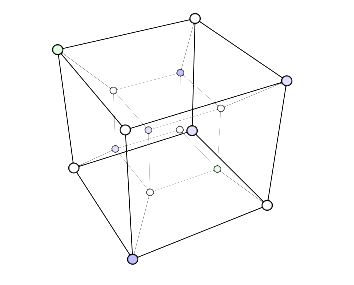
これが超立方体と言うものなのだそうです…。正方形の4個の頂点はデカルト座標系で簡素に書き表すことができる。 $ (0,0) $ , $ (0,1) $ , $ (1,0) $ , $ (1,1) $ だ。同様に、立方体の8個の頂点は次のようになる。 $ (0,0,0) $ , $ (0,0,1) $ , $ (0,1,0) $ , $ (1,0,0) $ , $ (0,1,1) $ , $ (1,0,1) $ , $ (1,1,0) $ , $ (1,1,1) $ 。
そうなると、4次元の超立方体の16の頂点がどこにあるのかも簡単にわかるだろう。
$ (0,0,0,0) $ , $ (0,0,0,1) $ , $ (0,0,1,0) $ , $ (0,1,0,0) $ , $ (1,0,0,0) $ , $ (0,0,1,1) $ , $ (0,1,0,1) $ , $ (0,1,1,0) $ , $ (1,0,0,1) $ , $ (1,0,1,0) $ , $ (1,1,0,0) $ , $ (0,1,1,1) $ , $ (1,0,1,1) $ , $ (1,1,0,1) $ , $ (1,1,1,0) $ , $ (1,1,1,1) $ だ。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
![]()
| ★ 平日を充実させるために… | ☆ 実施状況 |
|---|---|
| 2階に上り降り時、懸垂1回 (ボルダリングの体力獲得) ランチ & 買い物前 |
できず |
| 数学の問題 1問 (物理学の数式の理解力の獲得) ランチ & 買い物の前後 |
チャート式 数学 青I:できず チャート式 数学 青A:できず チャート式 数学 青II:できず チャート式 数学 青B:できず 実用数学技能検定 要点整理2級:せず 実用数学技能検定 要点整理準1級:せず 数学の学習に取り組んだ時間:0時間00分 チャート式 新物理 物理基礎・物理:できず ゼロからの大学物理 熱力学と統計力学:できず 物理学の学習に取り組んだ時間:0時間00分 |
| そろばんの練習5問 (暗算の獲得) 夜、寝る前 |
加減算 できず 掛け算 せず |
| 規則正しい休日の生活 基本習慣 |
昨日・寝床に入った時間:23時30分 今朝・6時台に布団から出る:06時50分 朝 --- ブログの投稿 --- |
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |