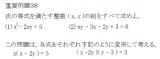みなさん、こんばんは。
数学の参考書 "改訂版 チャート式 解法と演習 数学Ⅰ+Aー数研出版" を進めていて気が付いたのですが、今まで私は「方程式を立てれば、後は計算を行うだけ」と言うイメージを数学自体に持っていました。しかしこれは間違った印象なのだと言う気がしてきました。例えば "改訂版 チャート式 解法と演習 数学Ⅰ+Aー数研出版" の６２ページの重要例題３８がその一例です。ちょっと見てみましょう。

答えは割愛しますが、ともかくこの重要例題は与式を変形する時に一工夫する必要があります。" x = **** " のような式の変形をするわけではなく、解答を探しやすくするための変形が必要です。
「解答にたどり着くためには与式を上記のように変形すれば良い」、と言う事は教えて貰えれば、後は分かる事ですが、なかなかこの「上記のように変形する」と言う考えが浮かびません。 "方程式を解く" と言う固定観念にとらわれていると特にそうでしょう。

因数分解の問題を解くための学習をしている時には、"公式を覚える" と言う事が一つスタイルでした。これがすなわち私の持っていた数学のイメージでした。しかしこれは序の口なのだと、ちょっと感じ始めた次第なのです。
数式を利用しながら、しかも考えなくてはならない。ましてや、数式をいろいろな問題を解く糸口にできるようにする。数式をいろいろな問題を解く時に利用出来るようになる！これが数学の勉強の本質でしょうかね。高校時代に参考書を一通り丁寧に学習した事が無かった私です。いまさら勉強不足だったのだなぁと、つくづく思ったりしております。
では、今日はこの辺で。