時空 解 さんの日記
2020
5月
10
(日)
09:13
本文
皆さん、おはようございます。時空 解です。
やっと互除法の証明が納得できました。4月の15日に理解したつもりだったんですけとね。
・数学の "証明" って、何?
・数学の "証明" って、何?
でも理解した証明を想い出して記述してみようと試みましたが、できず仕舞い…。
やっぱり自分の物にはなっていません。
やっぱり自分の物にはなっていません。
どうして互除法の証明にこだわっているのかと申しますと、ガロアの群論を理解しようと思って読み始めた書籍:「ガロア理論の頂を踏む」の冒頭部分に、この互除法の証明が載っているのです。(もちろんネット上にも多々あります) ですからガロアが築いた群論を理解するにはどうしても明確に理解したい気持ちがあるんですよね。でも未だに四苦八苦しているところです。手ごわいです、互除法を理解するのって。
なにが一番難しいかと言えば、きっと最初に仮定している「2つの最大公約数」 $ g $ と $ h $ の大小関係が $ g = h $ と解釈できるその理由でしょう。
今一度 証明を書籍:「ガロア理論の頂を踏む」から引用してみましょう。
今一度 証明を書籍:「ガロア理論の頂を踏む」から引用してみましょう。
証明
$ (a,~b) = g, (b,~r) = h $ とおいて、実は $ g = h $ であることを示しましよう。
$ a,b $ は $ g $ の倍数なので、自然数 $ a',b' $ を用いて、
$ a = a'g,~b = b'g …(1) $
と書くことができます。
$ a $ を $ b $ で割った商を $ q $ とします。余りが $ r $ ですから、
$ a = qb + r …(2) $ これより、$ r = a - qb $
これに $ (1) $ を代入して、$ r = a'g - qb'g = (a' - qb')g $
となり $ r $ も $ g $ を約数として持ちます。もともと $ b $ は $ g $ を約数として持ちますから、$ g $ は $ b $ と $ r $ の公約数です。公約数は最大公約数以下ですから、
$ g \leqq h $ です。
また、$b, r $ は $ h $ の倍数なので、自然数 $ c', r' $ を用いて、
$ b = c'h, r = r'h $
と書くことができます。$ (2) $ にこれを代入して、
$ a = qb + r = qc'h + r'h = (qc' + r')h $
$ a $ は $ h $ を約数に持ちます。$ b $ はもともと $ h $ を約数に持ちますから、$ h $ は $ a $ と $ b $ の公約数です。公約数は最大公約数以下なので、$ g \geqq h $ です。
$ g \leqq h $ かつ $ g \geqq h $ が示されたので、$ g = h $ です。
(証明終わり)
これを明確に理解するには下記の図が助けになるでしょう。参考にしてみて下さい。
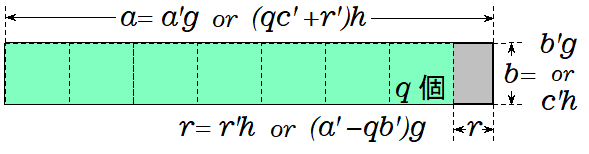
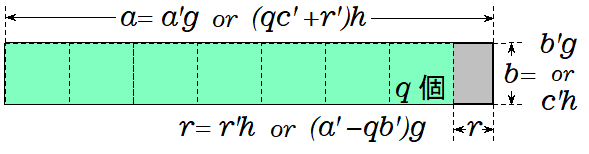
では今日も休日を始めます。休日の充実こそ、人生の充実です。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 平日を充実させるために… | ☆ 実施状況 |
|---|---|
| 2階に上り降り時、懸垂1回 (ボルダリングの体力獲得) ランチ & 買い物前 |
できず |
| 数学の問題 1問 (物理学の数式の理解力の獲得) ランチ & 買い物の前後 |
数学の学習に取り組んだ時間:1時間34分 物理学の学習に取り組んだ時間:0時間00分 |
| そろばんの練習 |
加減算 11~110の足し算1回、引き算 できず 掛け算 せず |
| 規則正しい休日の生活 基本習慣 |
昨日・寝床に入った時間:23時20分 今朝・6時台に布団から出る:06時15分 朝 --- ブログの投稿 --- |
閲覧(8015)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



