時空 解 さんの日記
2020
7月
29
(水)
08:56
本文
皆さん、おはようございます。時空 解です。
直角2等辺三角形の辺の長さを求めるのに、ピタゴラスの定理を使いますよね…でも、その結果が二重根号になった場合、皆さんはどうされますかね?
例えば下記のような直角二等辺三角形の場合です。
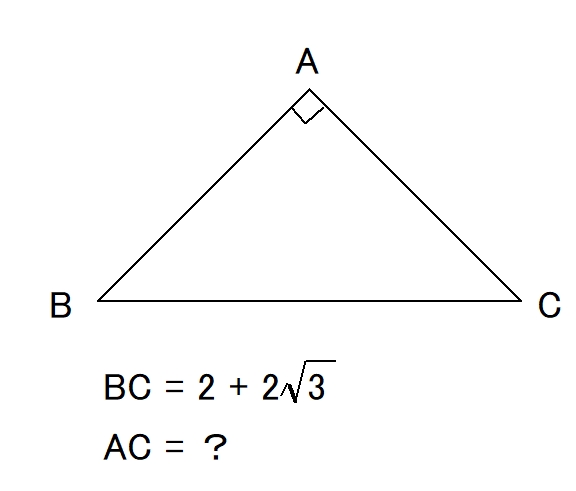
辺$ AB $ を求める方程式は
$ (2 + 2\sqrt{ 3 })^2 = 2(AB)^2 $
と考えますよね。そうすると $ AB $ の長さは
$ AB = \sqrt{ 8 + 4\sqrt{ 3 } } $
なんて数値になってしまいます。
なんとか2重根号を外したいところですが…うーむ…難しい。
と悩んだのですがこれはピタゴラスの定理を使って $ AB $ の長さを求めてしまったからいけないのですよね。
2重根号はどうやって外すんだったかなぁ…なんて悩み出すと他の方法に気が付かなくなって行きます。
これは三角比の関係、$ AB : BC = 1 : \sqrt{ 2 } $ を知っていれば簡単。
内項 $ \cdot $ 外項 は等しかったんですよね。これに気が付かなかった私は時間を無駄にしました。
$ 2 + 2\sqrt{ 3 } = \sqrt{ 2 } \cdot AB $
上式から $ AB $ を求めるだけでいいのです。ピタゴラスの定理を使うと言うバカの一つ覚えにハマった私でした。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
直角2等辺三角形の辺の長さを求めるのに、ピタゴラスの定理を使いますよね…でも、その結果が二重根号になった場合、皆さんはどうされますかね?
例えば下記のような直角二等辺三角形の場合です。

辺$ AB $ を求める方程式は
$ (2 + 2\sqrt{ 3 })^2 = 2(AB)^2 $
と考えますよね。そうすると $ AB $ の長さは
$ AB = \sqrt{ 8 + 4\sqrt{ 3 } } $
なんて数値になってしまいます。
なんとか2重根号を外したいところですが…うーむ…難しい。
と悩んだのですがこれはピタゴラスの定理を使って $ AB $ の長さを求めてしまったからいけないのですよね。
2重根号はどうやって外すんだったかなぁ…なんて悩み出すと他の方法に気が付かなくなって行きます。
これは三角比の関係、$ AB : BC = 1 : \sqrt{ 2 } $ を知っていれば簡単。
内項 $ \cdot $ 外項 は等しかったんですよね。これに気が付かなかった私は時間を無駄にしました。
$ 2 + 2\sqrt{ 3 } = \sqrt{ 2 } \cdot AB $
上式から $ AB $ を求めるだけでいいのです。ピタゴラスの定理を使うと言うバカの一つ覚えにハマった私でした。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 習慣作りのための、小さな課題 | ☆ 実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿後 |
加減算:できず |
| 2階に上り降り時、懸垂1回 (ボルダリングの体力獲得) ブログ投稿後 |
できず |
| 理数系の問題 1問 (物理学の数式の理解力の獲得) 90分 |
数学の学習に取り組んだ時間:0時間30分 |
| 規則正しい生活 基本習慣 |
昨日・寝床に入った時間:23時40分 今朝・6時台に布団から出る:07時10分 朝 --- 数学の学習 --- |
閲覧(8263)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



