時空 解 さんの日記
2020
10月
30
(金)
10:29
マスペディア 277 焦点と準線
 前の日記
次の日記
前の日記
次の日記 カテゴリー
マスペディア 1000
カテゴリー
マスペディア 1000
本文
皆さんこんにちは時空 解です。
今日は久々にマスペディアを開いてみました今日はトピック 277 です。焦点と準線。
ここのトピックを見て驚きましたね。皆さんは焦点と準線と聞いて何をイメージしますか?私はトンとイメージが湧きませんでしたので、まずはパソコンで検索、とりあえずは、Wikipedia を参照してみました。 なんだこりゃ…?
なんだこりゃ…?
もしもマスペディアのトピックを見ずにこの解説だけを読んでいたなら、何もイメージできていないでしょう。解説にある
「円錐曲線は焦点からの距離を準線からの距離で割った値(離心率 e)」
と言う一文が私を寄せ付けません。
図を使って解説をしてくれないとねぇ…Wikipedia の解説文で離心率を理解できる方がいらっしゃるのなら、とても尊敬する次第であります。
さて、マスペディアに載っている図はどんな物かと申しますと、同じような意味合いの図が、下記のサイトに載っていましたので、ここで示します。
・準線焦点と放物線 放物線の基本性質
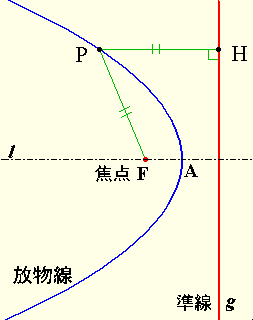 このサイトの図 (右に示しました) から離心率を示すならば、
このサイトの図 (右に示しました) から離心率を示すならば、
$ e = \displaystyle \frac{ PF }{ PH } $
です。こうして図と数式が示されていれば、準線と離心率と言うもののイメージし易いですよね。まぁ曲線がどんな曲線になるのかまではイメージできませんが…。
軌跡と言う単語は連想しますよね。
結局、下記のように整理できます。
0 < e < 1 ならば楕円:頂点までの距離を準線までの距離の例えば半分にした結果できる曲線
e = 1 ならば放物線:頂点までの距離と準線までの距離が等しい点を集めた曲線
e > 1 ならば双曲線:頂点までの距離を準線までの距離を例えば 1.2倍にした結果できる曲線
考えてみると、準線と言う単語があまり馴染みのない単語ですよね。まぁ勉強不足だって言われれば、言い返せませんが…とほほ。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
今日は久々にマスペディアを開いてみました今日はトピック 277 です。焦点と準線。
ここのトピックを見て驚きましたね。皆さんは焦点と準線と聞いて何をイメージしますか?私はトンとイメージが湧きませんでしたので、まずはパソコンで検索、とりあえずは、Wikipedia を参照してみました。
うーむ…・焦点 (幾何学) 1.2:焦点と X 線を用いた定義
任意の円錐曲線は、一つの焦点と一つの準線(これは焦点を含まない直線の形で与えられる)を用いて記述することもできる。 すなわち、円錐曲線は焦点からの距離を準線からの距離で割った値(離心率 e)が一定であるような点の軌跡として定義される。各円錐曲線は、離心率 e が
0 < e < 1 ならば楕円、
e = 1 ならば放物線、
e > 1 ならば双曲線
になる。焦点までの距離を固定して、準線を無限遠直線(英語版)へ飛ばせば離心率は 0 となり、円錐曲線は円になる。
もしもマスペディアのトピックを見ずにこの解説だけを読んでいたなら、何もイメージできていないでしょう。解説にある
「円錐曲線は焦点からの距離を準線からの距離で割った値(離心率 e)」
と言う一文が私を寄せ付けません。
図を使って解説をしてくれないとねぇ…Wikipedia の解説文で離心率を理解できる方がいらっしゃるのなら、とても尊敬する次第であります。
さて、マスペディアに載っている図はどんな物かと申しますと、同じような意味合いの図が、下記のサイトに載っていましたので、ここで示します。
・準線焦点と放物線 放物線の基本性質
 このサイトの図 (右に示しました) から離心率を示すならば、
このサイトの図 (右に示しました) から離心率を示すならば、$ e = \displaystyle \frac{ PF }{ PH } $
です。こうして図と数式が示されていれば、準線と離心率と言うもののイメージし易いですよね。まぁ曲線がどんな曲線になるのかまではイメージできませんが…。
軌跡と言う単語は連想しますよね。
結局、下記のように整理できます。
0 < e < 1 ならば楕円:頂点までの距離を準線までの距離の例えば半分にした結果できる曲線
e = 1 ならば放物線:頂点までの距離と準線までの距離が等しい点を集めた曲線
e > 1 ならば双曲線:頂点までの距離を準線までの距離を例えば 1.2倍にした結果できる曲線
考えてみると、準線と言う単語があまり馴染みのない単語ですよね。まぁ勉強不足だって言われれば、言い返せませんが…とほほ。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
閲覧(9060)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |







