時空 解 さんの日記
2021
1月
20
(水)
09:41
本文
皆さんこんにちは、時空 解です。
今日はチェバの定理とメネラウスの定理を学習していました。
うーむ…本当に3角形の頂点 $ A,~B,~C $ と、線分の分点 $ P,~Q,~R $ と言う図を示すために記号に振り回されます。
ひとまずチェバの定理とメネラウスの定理の覚え方なんですが、文章としては簡単です。
・頂→分→頂で三角形をひとまわり
と言う一文で済みます。
この "頂" と言うのが三角形の頂点のことで、"分" と言うのが三角形の辺を分けている点のことですね。
青チャート式数学Aに載っている覚え方と言うものをここで示してみましょう。
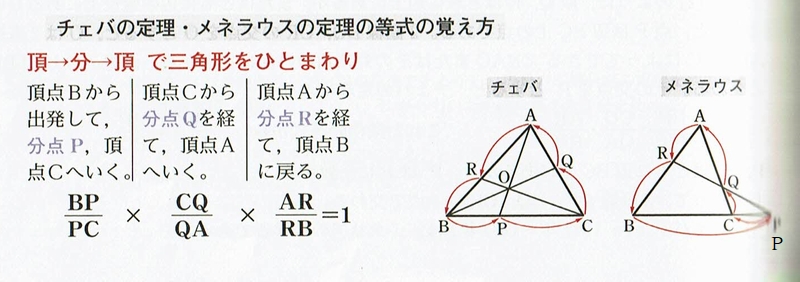
シンプルですが、さて、問題を解く時に上手く利用できるか否かですよね?
問題として出題されると、この3角形の頂点 $ A,~B,~C $ と、線分の分点 $ P,~Q,~R $ と言う記号の順番なんかが変えられたり、違うアルファベットが使われたりします。特にメネラウスの定理を使って解く問題などは、延長線の方向が3角形の右側に来るとは限っていませんよね。
そうすると、この覚え方で大丈夫なんだろうか? 問題と対応させて定理を利用するのが大変だなぁ…なんて想っていました。
問題と対応させて定理を利用するのが大変だなぁ…なんて想っていました。
でもこの不安は、青チャート式数学の基本例題76を解いてみると解消されますね。
本当に「頂→分→頂で三角形をひとまわり」と言うやり方で方程式を書き出せばいいことが分かります。
心配して損しました。
もしかしたら私がなにを心配していたのか、理解できない人が殆どかも知れませんね。(^^;
理解できた方からは「頭がカチカチだな」とも言われそうです。それにこの2つの定理の証明がちゃんと理解できていれば、私のようなか不安も感じずに、すぐに「頂→分→頂で三角形をひとまわり」と言うシンプル覚え方を素直り受け入れるでしょう。
まぁカチカチな頭だからこその不安は別として、次の2つ目の不安はどうでしょうかね? それは「分数の読み方」に関連することです。
チェバの定理とメネラウスの定理の覚え方は、分数を分子から分母へ読む形ですよね?これって私としては抵抗を感じるのですが、皆さんは如何てしょうか?
この定理の分数を分子から書くのか分母から書くのか…いざテストの時には迷ってしまう不安が付きまといます。
そう言えば、この点に付いては、以前も同じことを想ったんでした。想い出しました。
・分数の読み方、書き方の順番は、分母から?それとも分子から?
このときに一般的な分数の読み書き (分子から) と言うことに頭を切り替えたほうが良かったんですよね。
今回こそは、分数の読み書きを柔軟にして行きたいと想います。fx-JP900 と言う関数電卓の分数のキー入力も分子からですしね…
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
今日はチェバの定理とメネラウスの定理を学習していました。
うーむ…本当に3角形の頂点 $ A,~B,~C $ と、線分の分点 $ P,~Q,~R $ と言う図を示すために記号に振り回されます。
ひとまずチェバの定理とメネラウスの定理の覚え方なんですが、文章としては簡単です。
・頂→分→頂で三角形をひとまわり
と言う一文で済みます。
この "頂" と言うのが三角形の頂点のことで、"分" と言うのが三角形の辺を分けている点のことですね。
青チャート式数学Aに載っている覚え方と言うものをここで示してみましょう。

シンプルですが、さて、問題を解く時に上手く利用できるか否かですよね?
問題として出題されると、この3角形の頂点 $ A,~B,~C $ と、線分の分点 $ P,~Q,~R $ と言う記号の順番なんかが変えられたり、違うアルファベットが使われたりします。特にメネラウスの定理を使って解く問題などは、延長線の方向が3角形の右側に来るとは限っていませんよね。
そうすると、この覚え方で大丈夫なんだろうか?
でもこの不安は、青チャート式数学の基本例題76を解いてみると解消されますね。
本当に「頂→分→頂で三角形をひとまわり」と言うやり方で方程式を書き出せばいいことが分かります。
心配して損しました。
もしかしたら私がなにを心配していたのか、理解できない人が殆どかも知れませんね。(^^;
理解できた方からは「頭がカチカチだな」とも言われそうです。それにこの2つの定理の証明がちゃんと理解できていれば、私のようなか不安も感じずに、すぐに「頂→分→頂で三角形をひとまわり」と言うシンプル覚え方を素直り受け入れるでしょう。
まぁカチカチな頭だからこその不安は別として、次の2つ目の不安はどうでしょうかね? それは「分数の読み方」に関連することです。
チェバの定理とメネラウスの定理の覚え方は、分数を分子から分母へ読む形ですよね?これって私としては抵抗を感じるのですが、皆さんは如何てしょうか?
この定理の分数を分子から書くのか分母から書くのか…いざテストの時には迷ってしまう不安が付きまといます。
そう言えば、この点に付いては、以前も同じことを想ったんでした。想い出しました。
・分数の読み方、書き方の順番は、分母から?それとも分子から?
このときに一般的な分数の読み書き (分子から) と言うことに頭を切り替えたほうが良かったんですよね。
今回こそは、分数の読み書きを柔軟にして行きたいと想います。fx-JP900 と言う関数電卓の分数のキー入力も分子からですしね…
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(9325)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



