皆さんこんにちは、時空 解です。

表題に示した参考書、青チャート式数学Ａの第３章１１節にチェバの定理・メネラウスの定理の証明が載っていますが、「チェバの定理の逆の証明」に引っかかっていました。

まずはそのページを下記に示してみましょう。

まぁ逆の証明の前に、チェバの定理の証明そのものも理解するのにもちょっと苦労しましたけどね。　でも昨日やっと、逆の証明の方も理解できた次第です。

混乱を招く分部は下記の一文。
「$ \angle BAC $ またはその対頂角の内部にあるから,…」

この "対頂角の内部" と言うのはどこを指しているのかピンと来なかったんです。
もしかしたら皆さんも、直ぐには分らないのではないでしょうか？
でもその理由は簡単なことですよね、図が足りないんです。

私は図があるものとして文章を読んでいたので途方に暮れていました。
でも無いんですよね、このページには…

もし下の図が [2] のところにもう一つあれば途方に暮れることはありませんでした。


皆さんもこれで「チェバの定理の逆の証明」が分かり易くなったことと想いたいです。


さて、もう一つこの「チェバの定理の逆の証明」で分かり難いのは下記の一文ですよね。
「これと条件の等式から」

この "条件の" と言うものが私の頭の中ではクエスチョンマークでした。どこに条件があるのか、ピンと来なかったんです。
でもこれって、

　　　　　$ BQ $ と $ CR $ が交わり、かつ $ \displaystyle \frac{ BP }{ PC } \cdot  \frac{ CQ }{ QA } \cdot \frac{ AR }{ RB } = 1 $が成り立つならば、

と言う "成り立つならば、" が条件になっているのですよね。と言うことは

　　　　　$ \displaystyle \frac{ BP }{ PC } \cdot  \frac{ CQ }{ QA } \cdot \frac{ AR }{ RB } = \frac{ BP' }{ P'C } \cdot  \frac{ CQ }{ QA } \cdot \frac{ AR }{ RB } = 1 $

となり、$ P' $ は $ P $ と一致する、と言う解釈で良いのでしょう。
分かってしまえば簡単なことなんですが、私としてはどうにも言い回しに違和感があった次第でした。


まぁとにもかくにも、「チェバの定理の逆の証明」の疑問点が一通りクリアされたので、最後に追加した図形、点 $ O $ が $ \angle BAC $ の対頂角の内部にある場合に付いても、チェバの定理が成り立つっていることを観て行きましょう。

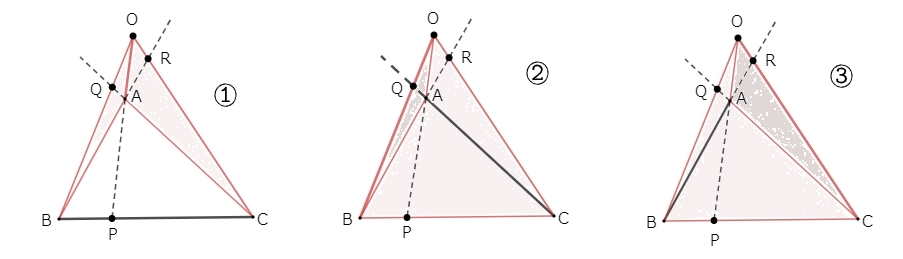
証明するためには下記の三つの等式が成り立てば良かったんですよね。

　　　　　$ \displaystyle \frac{ \triangle OAB }{ \triangle OCA } = \frac{ BP }{ PC } ……(1) $

　　　　　$ \displaystyle \frac{ \triangle OBC }{ \triangle OAB } = \frac{ CQ }{ QA } ……(2) $

　　　　　$ \displaystyle \frac{ \triangle OCA }{ \triangle OBC } = \frac{ AR }{ RB } ……(3) $

下記の図を参考に、３角形の共通の底辺と、それぞれの高さに注目してみてみてくださいね。


では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。