時空 解 さんの日記
2021
2月
1
(月)
09:54
本文
皆さんこんにちは、時空 解です。
図を観て、直感的に当たり前だと想えることを証明するのは結構厄介ですよね。
それを実感した問題があります。
それが下記の問題。青チャート式数学Aの基本例題80です。
 この問題はともに「三角形の辺と角の大小関係」を利用して証明するのですが…。
この問題はともに「三角形の辺と角の大小関係」を利用して証明するのですが…。
この問題の (1) も (2) もなんだか当たり前にみえた私です。
それでとにかく
「角と辺の関係を利用しないと証明にならないんだからなぁ…」
と想い、ひとまず (1) については下記のような証明を考えたんですよね。
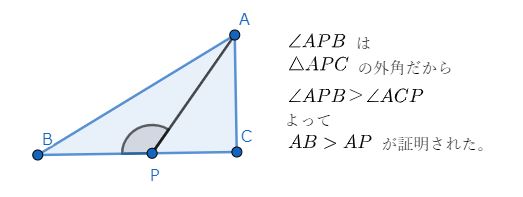
でもこれって全然ダメですよね。直ぐにそれは判ったのですがどうしてダメなのか?
その納得の行く理由を見付けるのにちょっと苦労しました。
ダメな理由は
「一つの三角形について、辺と角の大小関係を利用していない」
からですよね。
私の証明だと、$ \triangle ABC $ と $ \triangle ABP $ の2つの三角形にまたがって角の大小関係を比較しています。
これでは辺と無関係な角の大小関係を言っているのです。2つの三角形がどのような関係にあるのかを明確にしてからでないと証明になりません。
「三角形の辺と角の大小関係」は1つの三角形に付いて言える定理ですよね…それが明確に分っていなかった私でした。
バカですよねぇ…。_| ̄|○
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
図を観て、直感的に当たり前だと想えることを証明するのは結構厄介ですよね。
それを実感した問題があります。
それが下記の問題。青チャート式数学Aの基本例題80です。
 この問題はともに「三角形の辺と角の大小関係」を利用して証明するのですが…。
この問題はともに「三角形の辺と角の大小関係」を利用して証明するのですが…。
この問題の (1) も (2) もなんだか当たり前にみえた私です。
それでとにかく
「角と辺の関係を利用しないと証明にならないんだからなぁ…」
と想い、ひとまず (1) については下記のような証明を考えたんですよね。

でもこれって全然ダメですよね。直ぐにそれは判ったのですがどうしてダメなのか?
その納得の行く理由を見付けるのにちょっと苦労しました。
ダメな理由は
「一つの三角形について、辺と角の大小関係を利用していない」
からですよね。
私の証明だと、$ \triangle ABC $ と $ \triangle ABP $ の2つの三角形にまたがって角の大小関係を比較しています。
これでは辺と無関係な角の大小関係を言っているのです。2つの三角形がどのような関係にあるのかを明確にしてからでないと証明になりません。
「三角形の辺と角の大小関係」は1つの三角形に付いて言える定理ですよね…それが明確に分っていなかった私でした。
バカですよねぇ…。_| ̄|○
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(9143)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



