時空 解 さんの日記
2021
4月
3
(土)
09:43
本文
皆さんこんにちは、時空 解です。
昨日も数検2級2次のための学習を進めていました。昨日やっていたのが「実用数学技能検定要点整理2級」の 「5-3 不定積分と定積分」のところです。
この節で一番悩ましいのが表題にも示しました数式
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
ではないでしょうか?
告白いたしますと、この数式を数年前にもみているのですが頭の中が真っ白になるものですから…飛ばしてたんです。
「こんなの直ぐに理解できる訳がない…」
と、無意識のうちに直感してたんでしょうね、理解しようと言う気にも成りませんでした。
取っ付き難いですよね、この数式。 Φ(― ― ) .。うーむ
左辺では変数 $ t $ で積分しているのに、右辺を見ると変数が $ x $ 。
私に取ってはこの点がもっとも混乱を感じるところでした。この数日間、この混乱をどう乗り越えるのか試行錯誤をしてたんです。
それで単純化を想い出しました。これは以前、ここの会員さんから頂いたアドバイスです。
それが功を奏しました。それなりに理解が進んだんです。
今日はこのことに付いて書いてみたいと想います。
私が行ったのは $ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $ の式の左辺をシンプルな式に置き換えることす。
さて皆さん、この置き換えによる流れを見てどう思われましたか?
何の意味もないような計算でしたが、1つの変数 $ t $ に、定数 $ a $ と変数 $ x $ をそれぞれ代入することで変数 $ t $ が消去されたことは分かりましたよね?
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
の数式にある $ f(t) $ はこんな理由で消えても良いのがこの置き換えで納得できました。まぁこの置き換え算術に何か意味があるのか、はたまた正しいのか…それは定かではありませんが…
ともかく
「変数に "定数" と "別の変数" をそれぞれ代入しているんだなぁ」
と言うのが見通せて混乱が治まりました。
さて、ここで改めて
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
を利用して解く問題に付いて考えてみましょう。
例として「要点整理2級」の p113 「練習問題4」を取り上げてみます。
上記のように問題文の与式は、先頭に $ \displaystyle \frac{ d }{ dx } $ が抜けている形で出題されてきます。
とにかく $ f(x) $ を求めるために
と機械的に求めることができます。
でもこの問題…何のために $ f(x) $ を求めたのでしょうか?
そんな疑問は残りますよね…。うーむ、これも気持ちが悪い。でも一応、最後まで解いておきましょうね。
$ a $ は、問題の与式 $ \displaystyle \int_{a}^{x} f(t) dt = x^2 -2x -3 $ の $ x $ に $ a $ を代入すると求められます。
さて、ここで改めて問題の与式を見てみましょう。
$ \displaystyle \int_{a}^{x} f(t) dt = x^2 -2x -3 $
これが定積分の形をしていますから、グラフ上では面積と想っていいですよね。
これを $ S $ とでもしましょう。
$ S = x^2 -2x -3 $
$ f(t) = 2t -2 $
この2つがどんな関係にあるのか…? ちょっと考えてみて下さい。
ピンときましたか?
微分のところで曲線から「接線の方程式」を求めましたよね。今回は面積 $ S $ から「面積を挟む線の方程式」を求めているのではないか…
そんな想像が出来たりしませんか?
「面積を挟む線の方程式」と言う表現が分かり難いと想いますので、実際に確認してみましょう。
確認するために Geogebra を使って $ f(t) = 2t -2 $ と $ S = x^2 -2x -3 $ のグラフを書いてみました。
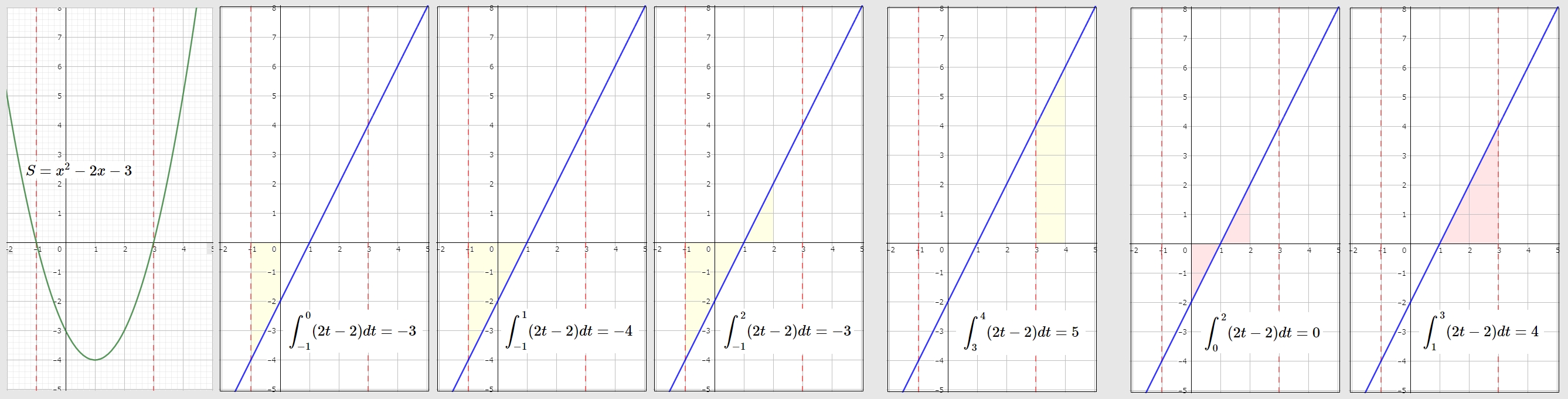
一番左側に
$ S = x^2 -2x -3 $
のグラフ
その隣には
$ f(t) = 2t -2 $
直線 (青線) と $ x $ 軸とで囲まれる面積 (黄色) を示しました。この黄色で示した部分が
$ \displaystyle \int_{a}^{ x } f(t) dt $
ですよね。
黄色で示した部分の量は、確かに$ S = x^2 -2x -3 $ のグラフと一致しています。
この「練習問題4」を解くと言うことは、曲線の接線方程式を求めること同じようなものなんですね。
これで
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
の式が素直に受け入れられるようになりました。もう頭の中は真っ白にはなりません。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
昨日も数検2級2次のための学習を進めていました。昨日やっていたのが「実用数学技能検定要点整理2級」の 「5-3 不定積分と定積分」のところです。
この節で一番悩ましいのが表題にも示しました数式
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
ではないでしょうか?
告白いたしますと、この数式を数年前にもみているのですが頭の中が真っ白になるものですから…飛ばしてたんです。
「こんなの直ぐに理解できる訳がない…」
と、無意識のうちに直感してたんでしょうね、理解しようと言う気にも成りませんでした。
取っ付き難いですよね、この数式。 Φ(― ― ) .。うーむ
左辺では変数 $ t $ で積分しているのに、右辺を見ると変数が $ x $ 。
私に取ってはこの点がもっとも混乱を感じるところでした。この数日間、この混乱をどう乗り越えるのか試行錯誤をしてたんです。
それで単純化を想い出しました。これは以前、ここの会員さんから頂いたアドバイスです。
それが功を奏しました。それなりに理解が進んだんです。
今日はこのことに付いて書いてみたいと想います。
私が行ったのは $ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $ の式の左辺をシンプルな式に置き換えることす。
~ 置き換え ~
$ t,~x $ は変数。$ a $ は定数です。左辺を定積分でも微分でもない $ 4t + a $ と言う式に置き換えます。右辺の $ f(x) $ は適当に $ x^2 -2x -3 $ とでもしましょう。
すると
$ 4t + a = x^2 -2x -3 $
上式に対して下記の2つの条件が同時に成り立つとします。
・$ t = x $
・$ t = a $
(これって、つまりは $ x = a $ と言うことですけどね)
上の2つの条件をそれぞれを与式に代入すると
$ 4x + a = x^2 -2x -3 $ …($ \alpha $)
$ 4a + a = x^2 -2x -3 $ …($ \beta $)
の2つを得ますよね。
これを連立一次方程式として解くと、($ \alpha ) - ( \beta $) で $ 4x - 4a = 0 $ となりますから $ x = a $ が直ぐに出て来ます。
$ t,~x $ は変数。$ a $ は定数です。左辺を定積分でも微分でもない $ 4t + a $ と言う式に置き換えます。右辺の $ f(x) $ は適当に $ x^2 -2x -3 $ とでもしましょう。
すると
$ 4t + a = x^2 -2x -3 $
上式に対して下記の2つの条件が同時に成り立つとします。
・$ t = x $
・$ t = a $
(これって、つまりは $ x = a $ と言うことですけどね)
上の2つの条件をそれぞれを与式に代入すると
$ 4x + a = x^2 -2x -3 $ …($ \alpha $)
$ 4a + a = x^2 -2x -3 $ …($ \beta $)
の2つを得ますよね。
これを連立一次方程式として解くと、($ \alpha ) - ( \beta $) で $ 4x - 4a = 0 $ となりますから $ x = a $ が直ぐに出て来ます。
さて皆さん、この置き換えによる流れを見てどう思われましたか?
何の意味もないような計算でしたが、1つの変数 $ t $ に、定数 $ a $ と変数 $ x $ をそれぞれ代入することで変数 $ t $ が消去されたことは分かりましたよね?
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
の数式にある $ f(t) $ はこんな理由で消えても良いのがこの置き換えで納得できました。まぁこの置き換え算術に何か意味があるのか、はたまた正しいのか…それは定かではありませんが…
ともかく
「変数に "定数" と "別の変数" をそれぞれ代入しているんだなぁ」
と言うのが見通せて混乱が治まりました。
さて、ここで改めて
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
を利用して解く問題に付いて考えてみましょう。
例として「要点整理2級」の p113 「練習問題4」を取り上げてみます。
p113 練習問題4
次の等式を満たす関数 $ f(x) $ と定数 $ a $ の値を求めなさい。
$ \displaystyle \int_{a}^{x} f(t) dt = x^2 -2x -3 $
次の等式を満たす関数 $ f(x) $ と定数 $ a $ の値を求めなさい。
$ \displaystyle \int_{a}^{x} f(t) dt = x^2 -2x -3 $
上記のように問題文の与式は、先頭に $ \displaystyle \frac{ d }{ dx } $ が抜けている形で出題されてきます。
とにかく $ f(x) $ を求めるために
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
を利用して
$ \displaystyle { f(x) = \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = 2x -2 } $
$ \therefore f(t) = 2t -2 $
を利用して
$ \displaystyle { f(x) = \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = 2x -2 } $
$ \therefore f(t) = 2t -2 $
と機械的に求めることができます。
でもこの問題…何のために $ f(x) $ を求めたのでしょうか?
そんな疑問は残りますよね…。うーむ、これも気持ちが悪い。でも一応、最後まで解いておきましょうね。
$ a $ は、問題の与式 $ \displaystyle \int_{a}^{x} f(t) dt = x^2 -2x -3 $ の $ x $ に $ a $ を代入すると求められます。
$ \displaystyle \int_{a}^{a} f(t) dt = 0 $
なので
$ a^2 -2a -3 = 0 $
が言える。
因数分解すると
$ (a -3)(a +1) = 0 $
$ \therefore a= -1,~3 $
なので
$ a^2 -2a -3 = 0 $
が言える。
因数分解すると
$ (a -3)(a +1) = 0 $
$ \therefore a= -1,~3 $
さて、ここで改めて問題の与式を見てみましょう。
$ \displaystyle \int_{a}^{x} f(t) dt = x^2 -2x -3 $
これが定積分の形をしていますから、グラフ上では面積と想っていいですよね。
これを $ S $ とでもしましょう。
$ S = x^2 -2x -3 $
$ f(t) = 2t -2 $
この2つがどんな関係にあるのか…? ちょっと考えてみて下さい。
ピンときましたか?
微分のところで曲線から「接線の方程式」を求めましたよね。今回は面積 $ S $ から「面積を挟む線の方程式」を求めているのではないか…
そんな想像が出来たりしませんか?
「面積を挟む線の方程式」と言う表現が分かり難いと想いますので、実際に確認してみましょう。
確認するために Geogebra を使って $ f(t) = 2t -2 $ と $ S = x^2 -2x -3 $ のグラフを書いてみました。

一番左側に
$ S = x^2 -2x -3 $
のグラフ
その隣には
$ f(t) = 2t -2 $
直線 (青線) と $ x $ 軸とで囲まれる面積 (黄色) を示しました。この黄色で示した部分が
$ \displaystyle \int_{a}^{ x } f(t) dt $
ですよね。
黄色で示した部分の量は、確かに$ S = x^2 -2x -3 $ のグラフと一致しています。
$ a = -1 $ の場合
$ \displaystyle \int_{-1}^{ 0 } (2t-2) dt = -3 $ $ x^2 -2x -3 = -3 $
$ \displaystyle \int_{-1}^{ 1 } (2t-2) dt = -4 $ $ x^2 -2x -3 = -4 $
$ \displaystyle \int_{-1}^{ 2 } (2t-2) dt = -3 $ $ x^2 -2x -3 = -3 $
$ a = 3 $ の場合
$ \displaystyle \int_{3}^{ 4 } (2t-2) dt = 5 $ $ x^2 -2x -3 = 5 $
でも、$ a = 0 $ とか $ a = 1 $ の場合は成立しません。
$ \displaystyle \int_{0}^{ 2 } (2t-2) dt = 0 $ $ x^2 -2x -3 = -3 $
$ \displaystyle \int_{1}^{ 3 } (2t-2) dt = 4 $ $ x^2 -2x -3 = 0 $
$ \displaystyle \int_{-1}^{ 0 } (2t-2) dt = -3 $ $ x^2 -2x -3 = -3 $
$ \displaystyle \int_{-1}^{ 1 } (2t-2) dt = -4 $ $ x^2 -2x -3 = -4 $
$ \displaystyle \int_{-1}^{ 2 } (2t-2) dt = -3 $ $ x^2 -2x -3 = -3 $
$ a = 3 $ の場合
$ \displaystyle \int_{3}^{ 4 } (2t-2) dt = 5 $ $ x^2 -2x -3 = 5 $
でも、$ a = 0 $ とか $ a = 1 $ の場合は成立しません。
$ \displaystyle \int_{0}^{ 2 } (2t-2) dt = 0 $ $ x^2 -2x -3 = -3 $
$ \displaystyle \int_{1}^{ 3 } (2t-2) dt = 4 $ $ x^2 -2x -3 = 0 $
この「練習問題4」を解くと言うことは、曲線の接線方程式を求めること同じようなものなんですね。
これで
$ \displaystyle { \frac{ d }{ dx } \int_{ a }^{ x } f(t) dt = f(x) } $
の式が素直に受け入れられるようになりました。もう頭の中は真っ白にはなりません。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(8286)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



