皆さんこんにちは、時空 解です。

昨日は過去に受検し、手元にある２級２次の過去問を解いてみました。解いたのは2019年9月28日に実施された 第342回のものです。

ここで特有問題を取り上げてみましょう。
特有問題と言うのは数学検定協会が言うところでは、思考力を要する問題、と言う定義でしょうかね。数学を使って解くパズルのような問題が多いです。

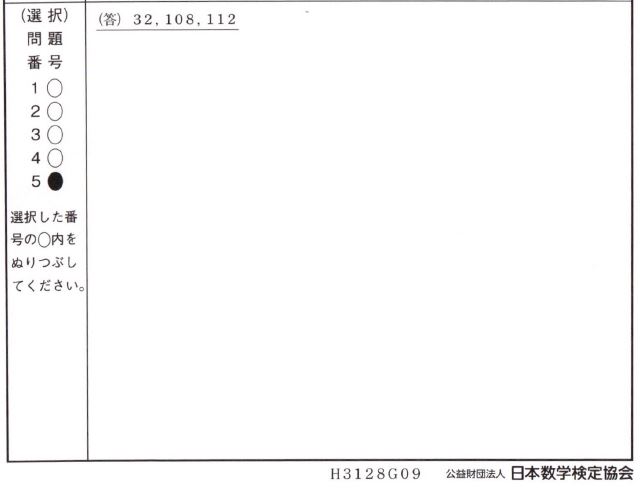
特有問題 (第342回の２級２次：選択問題５」
$ a,~b,~c $ を正の整数とし、縦 $ a $、横 $ b $、高さ $ c $ の直方体について考えます。この直方体の
対角線の長さが $ 9 $ のとき、直方体の体積 $ V $ のとり得る値は３つあります。それらをすべて求
めなさい。この問題は、解法の過程を記述せずに答えだけを書いてください。　　　　　　(整理技能)

実際に受検している時に想ったのですが、
「解けないなぁ…」
と、自分にがっがり…。＿|￣|○

中学時代の自分なら解いていただろうなぁ…なんて、そんなことも想っておりました。


検定結果が送られて来た時には「全体の正解率 ５９．３％」を観てさらにショックでしたね。

どうやって解くんだろうと想っていたんですが、検定結果の解答にも答が載っているだけ…解法は書かれていません。
この手の問題って、テスト後に友人に聞いても
「えっ！あの問題が解けなかったの？」
なんてニヤニヤされそうで、なかなか聞きずらいものですよね。(と想うのはわたしだけ？)

まぁとにかく今回、これがやっと解けた次第です。
解ける方は今日のブログの内容はつまらないでしょうけど、解けなかった方にはスッキリとして頂けるのではないでしょうか？
そう想って (私の解法でも良ければ) 書いてみました。


制約として下記の等式を満たす必要があります。
$ \sqrt{ a^2 + b^2 + c^2 } = 9 $

両辺を２乗して変形すると
$ 81 - c^2 = a^2 + b^2 $　　　…(1)

さて、ここからがポイントなんだと想いますが、２乗しても $ 81 $ を越えない整数、と言うのが重要になります。下記にそれを列記すると

$ 1^2 = 1 $
$ 2^2 = 4 $
$ 3^2 = 9 $
$ 4^2 = 16 $
$ 5^2 = 25 $
$ 6^2 = 36 $
$ 7^2 = 49 $
$ 8^2 = 64 $

の $ 1 $ から $ 8 $ までの８個ですよね。
こうして列記すると、直方体を構成する３辺 $ (a,~b,~c) $ の組み合わせは、上記の８個の中から (1) を満たす組み合わですから考え易いと想います。

2019年9月28日当時は、この整理が出来なかったんです。
上記の８個が明記できれば、後は下記の式を続いて列記し、解答に辿り着けます。
この下記の列記は $ c^2 $ に上記の８個をそれぞれ (1) に代入してできる数式です。

$ 81 - 1 = 80 = a^2 + b^2 $
$ 81 - 4 = 77 = a^2 + b^2 $
$ 81 - 9 = 72 = a^2 + b^2 $
$ 81 - 16 = 65 = a^2 + b^2 $
$ 81 - 25 = 56 = a^2 + b^2 $
$ 81 - 36 = 45 = a^2 + b^2 $
$ 81 - 49 = 32 = a^2 + b^2 $
$ 81 - 64 = 17 = a^2 + b^2 $

後は $ a^2 $ と $ b^2 $ の組み合わせで等式が成立する数はどれとどれなのか？
見通せますよね。

２つの数字の組み合わせを思考錯誤するのはそれほど大変ではありません。
(1) 式で考えても３つの数字の組み合わせから $ 81 $ を弾き出すのはなかなかの至難の業ですからね。
まぁノイマンとかチューリングなら簡単に出来るのでしょうが…。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。