時空 解 さんの日記
2016
6月
15
(水)
00:14
本文
みなさん、こんにちは。時空 解です。
さっそく数学の参考書「数学1高速トレーニング三角比編 (東進ブックス 大学受験 高速マスター)」の勉強は進めております。現在 Step01 から Step17 まで(第 1章と第2章)進めたところです。
正直、高校時代の自分がいかに勉強不足だったのかを痛感させられました。sin , cos , tan の定義はもちろん覚えていましたが、ただそれだけの事でした。それに sin , cos , tan の定義の覚え方…これがその後の三角比を学ぶのに大きく影響する事を体感できました。高校時代に利用した sin , cos , tan の覚え方、いわゆる一般的な記憶法に留まっていたのではダメです。
一般的な覚え方と「数学1高速トレーニング三角比編 (東進ブックス 大学受験 高速マスター)」の憶え方を比較してみましょう。
さっそく数学の参考書「数学1高速トレーニング三角比編 (東進ブックス 大学受験 高速マスター)」の勉強は進めております。現在 Step01 から Step17 まで(第 1章と第2章)進めたところです。
正直、高校時代の自分がいかに勉強不足だったのかを痛感させられました。sin , cos , tan の定義はもちろん覚えていましたが、ただそれだけの事でした。それに sin , cos , tan の定義の覚え方…これがその後の三角比を学ぶのに大きく影響する事を体感できました。高校時代に利用した sin , cos , tan の覚え方、いわゆる一般的な記憶法に留まっていたのではダメです。
一般的な覚え方と「数学1高速トレーニング三角比編 (東進ブックス 大学受験 高速マスター)」の憶え方を比較してみましょう。
・一般的な覚え方
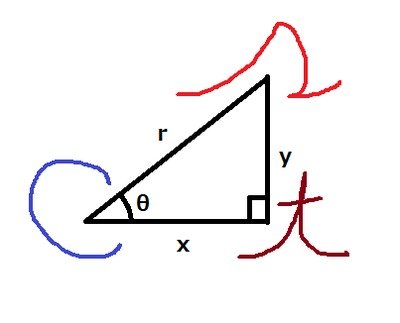
sin はSの筆記体を、三角形の斜辺と垂線になぞって r 分の y と覚える。
cos はCの文字を、三角形の斜辺と底辺になぞって r 分の x と覚える。
tan は t の筆記体を、三角形の底辺と垂線になぞって x 分の y と覚える。
・「数学1高速トレーニング三角比編 (東進ブックス 大学受験 高速マスター)」の覚え方
sin は「θ にへばりついていない辺」→「 x 座標」→ 180°と90°の変換は…と次々と出世させて行く。
cos は「θ にへばりついている辺」→「 y 座標」→ 180°と90°の変換は…と次々と出世させて行く。
tan は 「 sin/cos 」→「xy 座標グラフの傾き」→ 180°と90°の変換は…と次々と出世させて行く。
sin は「θ にへばりついていない辺」→「 x 座標」→ 180°と90°の変換は…と次々と出世させて行く。
cos は「θ にへばりついている辺」→「 y 座標」→ 180°と90°の変換は…と次々と出世させて行く。
tan は 「 sin/cos 」→「xy 座標グラフの傾き」→ 180°と90°の変換は…と次々と出世させて行く。
一般的な覚え方に留まっていると、θ の角度が 0 ≦ θ ≦ 90° の範囲にしかイメージが生まれません。sin , cos , tan の抽象化の威力が頭の中でイメージしにくくなるのです。
始めの一歩として一般的な覚え方をする事は必要ですが、その続きをトレーニングする事がとても大事になります。「数学1高速トレーニング三角比編 (東進ブックス 大学受験 高速マスター)」の言葉を借りるのならば sin , cos , tan の定義を次々と出世させて行く事が大切です。この書籍でも実は sin , cos の最初の定義「θに張り付いている、いない辺」と言う考え方は θ > 90° になるとイメージしにくくなります。そこで sin , cos と x 座標、y 座標の対応となるわけで、ここからプラスとマイナイの考え方も加味されて行きます。
三角比におけるマイナスの定義を納得(正しいと肌で感じる事が出来る)する事は始めは難しいでしょう。これは紀元前500年頃のピュタゴラス学派がマイナイの数字を納得する事に似ているかも知れません。
紀元前の時代、数学にマイナスと言う数字の概念は確立されていませんでした。と言うのもピュタゴラス学派の人たちにとって数字は、図形(土地の面積)に対応している概念だったからです。マイナスの数字は彼らにとっては、土地が無い事よりも少ない数字、と言う意味です。あり得ません。三角比における cosθ ( θ ≧ 90°) がどうしてマイナスになるのか?この疑問はまさにトレーニングで克服するものでしょう。三角比と言う抽象化の威力を発揮するための訓練なのだと割り切るしかないと思います。単位円の中心を x 座標と y 座標の交点と一緒にしてみて、さていろいろと演算を行ってみると、どうやら ± の関係とか sin と cos の相互変換が上手く行く…と言うような「抽象化するのに都合がいい」事を先人たちが見い出したと考えるのです。
と言う事で三角比をトレーニングして、その抽象化の醍醐味を味わって行きたいと思います。
始めの一歩として一般的な覚え方をする事は必要ですが、その続きをトレーニングする事がとても大事になります。「数学1高速トレーニング三角比編 (東進ブックス 大学受験 高速マスター)」の言葉を借りるのならば sin , cos , tan の定義を次々と出世させて行く事が大切です。この書籍でも実は sin , cos の最初の定義「θに張り付いている、いない辺」と言う考え方は θ > 90° になるとイメージしにくくなります。そこで sin , cos と x 座標、y 座標の対応となるわけで、ここからプラスとマイナイの考え方も加味されて行きます。
三角比におけるマイナスの定義を納得(正しいと肌で感じる事が出来る)する事は始めは難しいでしょう。これは紀元前500年頃のピュタゴラス学派がマイナイの数字を納得する事に似ているかも知れません。
紀元前の時代、数学にマイナスと言う数字の概念は確立されていませんでした。と言うのもピュタゴラス学派の人たちにとって数字は、図形(土地の面積)に対応している概念だったからです。マイナスの数字は彼らにとっては、土地が無い事よりも少ない数字、と言う意味です。あり得ません。三角比における cosθ ( θ ≧ 90°) がどうしてマイナスになるのか?この疑問はまさにトレーニングで克服するものでしょう。三角比と言う抽象化の威力を発揮するための訓練なのだと割り切るしかないと思います。単位円の中心を x 座標と y 座標の交点と一緒にしてみて、さていろいろと演算を行ってみると、どうやら ± の関係とか sin と cos の相互変換が上手く行く…と言うような「抽象化するのに都合がいい」事を先人たちが見い出したと考えるのです。
と言う事で三角比をトレーニングして、その抽象化の醍醐味を味わって行きたいと思います。
「θ」 と言う角度の一定量変化と「単位円上の x , y 量」と言う不定量変化の対応の仕方を一発で表現出来る抽象化の sin , cos , tan 。
この抽象化を踏まえてのシュレディンガー方程式の理解、解釈できるようになる事を今から楽しみにしたいところです。
では今日はこの辺で。
では今日はこの辺で。
独学協友会の動画は YouTube チャンネル でご覧になれます。
閲覧(14034)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



