時空 解 さんの日記
2016
7月
4
(月)
11:50
本文
みなさん、こんにちは。時空 解です。
「数学Ⅰ 高速トレーニング 三角比編」 を勉強しているところなのですが、"Step28 不等式を解いてみよう (sin 編)" で手こずりました。と言うのも二次不等式の解の求め方を学習したのが高校時代のみだったからです。"Step28 不等式を解いてみよう (sin 編)" は2次不等式に付いて学習しておかないと、ちょっと消化不良を起こす可能性があります。
内容は以下のような内容です。
「数学Ⅰ 高速トレーニング 三角比編」 を勉強しているところなのですが、"Step28 不等式を解いてみよう (sin 編)" で手こずりました。と言うのも二次不等式の解の求め方を学習したのが高校時代のみだったからです。"Step28 不等式を解いてみよう (sin 編)" は2次不等式に付いて学習しておかないと、ちょっと消化不良を起こす可能性があります。
内容は以下のような内容です。

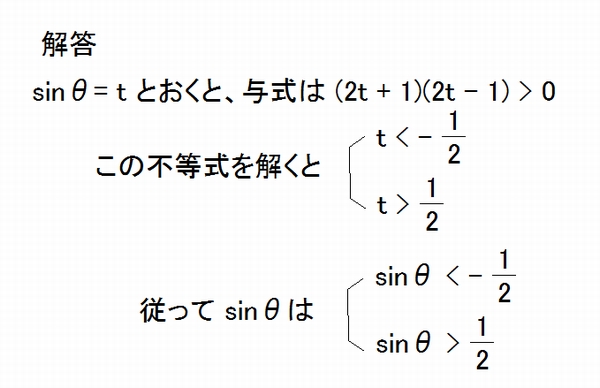
さて、この内容で因数分解された2次不等式が出て来ます。(2t + 1)(2t - 1) > 0 と言う式です。
① (2t + 1)(2t - 1) > 0 …問題で扱っている不等式
② (2t + 1)(2t - 1) < 0
この①と②の違いが分かりますか?
私はここで手こずりました。と言うのも t を求める2次方程式
私はここで手こずりました。と言うのも t を求める2次方程式
(2t + 1)(2t - 1) = 0
を解く要領で不等式を扱ってしまい、下記の二つを思い浮かべたからです。
2t + 1 > 0 → 2t > -1 → t > -1/2 …答えが違ってしまう。
2t - 1 > 0 → 2t > 1 → t > 1/2
しかし "赤チャート式の数学参考書 数学Ⅰ+A" の二次不等式のところを見て、頭の中を整理する事が出来た次第です。具体的には二次方程式のグラフを見て上記①と②の違いを納得しました。二次方程式は下記のようになります。
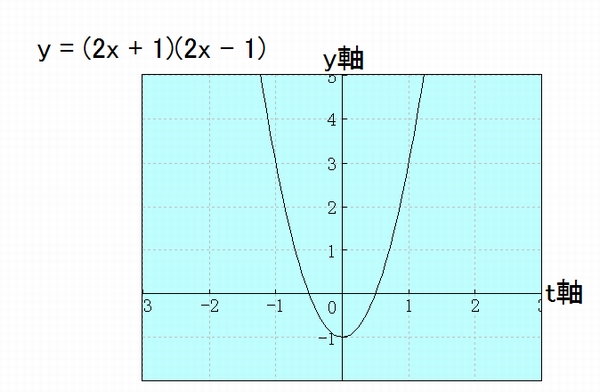
このグラフは縦軸が y に対応し、横軸には t が対応しています。
① (2t + 1)(2t - 1) > 0 は y 軸の 0 よりも上側の双曲線の部分となります。従って t は -1/2 未満、それと 1/2 より大きい値、この二つが解答となります。( もしかすると、これは中学数学のレベルの話かも知れませんね…自分の実力を思い知れられます)
この問題の与式は因数分解された形で示されているので、双曲線のイメージを頭に浮かべる事が出来るか、注意が必要ですね。
では今日はこの辺で。
この問題の与式は因数分解された形で示されているので、双曲線のイメージを頭に浮かべる事が出来るか、注意が必要ですね。
では今日はこの辺で。
独学協友会の動画は YouTube チャンネル でご覧になれます。
閲覧(10587)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



