時空 解 さんの日記
2016
8月
1
(月)
23:10
本文
みなさん、こんにちは。時空 解です。
今日は「数学Ⅰ 高速トレーニング 三角比編」と言う参考書の Step18 "入試問題にチャレンジ" を終えたところです。
うーむ、手ごたえがありました。「解けるまで一人で考え抜く」なんて気構えでやっていたらいつ終わるのかわからないくらいに難しかったです。( ^^;
今日は「数学Ⅰ 高速トレーニング 三角比編」と言う参考書の Step18 "入試問題にチャレンジ" を終えたところです。
うーむ、手ごたえがありました。「解けるまで一人で考え抜く」なんて気構えでやっていたらいつ終わるのかわからないくらいに難しかったです。( ^^;
それに式の展開公式や因数分解のパターンも知らない解けない問題が多くありました。まぁそれも当たり前ですかね、さすがに大学の入試問題から選んできた三角比関連の問題です。公式と、それ式の変形センスとでもいいましようかね、この二つがそろっていないと解けな問題です。
公式は下記の2つくらいを知っていれば大丈夫です。
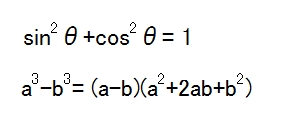
しかし問題が要求している解答に至るための試行錯誤と与式の変形の仕方には、なかなか辿れ付ける代物ではないと思います。
でも不思議なものですね、問題は20あるのですが、その解答を一通り経験すると、その次からは20の問題が結構ワンパターンな "試行錯誤と与式の変形" で解答出来る感覚を覚えます。
公式は下記の2つくらいを知っていれば大丈夫です。
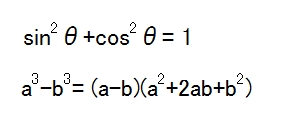
しかし問題が要求している解答に至るための試行錯誤と与式の変形の仕方には、なかなか辿れ付ける代物ではないと思います。
でも不思議なものですね、問題は20あるのですが、その解答を一通り経験すると、その次からは20の問題が結構ワンパターンな "試行錯誤と与式の変形" で解答出来る感覚を覚えます。
やっぱり数学の問題は「解けるまで一人で考え抜く」と言う姿勢でやると時間が掛かって仕方ありません。
それよりも多くのパターンを経験する事が大切です。
それよりも多くのパターンを経験する事が大切です。
三角比の問題を解いていて、ふと分数の計算方法について考えてしまいました。問題中に sin,cos,tan の分数計算やルートを含む分数計算が出てくるからです。その分数計算に付いて疑問が沸いてしまうほどに、"入試問題にチャレンジ" を始めた時は戸惑ったものです。
実は分数計算が現代のように簡単に出来るようになったのは、インド人がゼロの発見をして、数字を現代の位取り法と言う表記にしてくれたおかげです。ピタゴラス時代の分数計算と言えばそれは複雑だったのだそうです。現在では掛け算の時には分母と分母、それに分子と分子をそれぞれかけ合わせれば答えがでます。割り算の時には分母と分子、それに分子と分母を掛け合わせると答えがでます。しかし分数計算に sin,cos,tan やルートが絡んでくるとハタと考えてしまったのです。本当に上記の分数計算は正しいのだろうか?と。
あんまり考えすぎて、マイナスと言う数字自体に疑問を持ち始めるところでした。これじゃぁピタゴラス時代の人と同じレベルです。( ^^;
実は分数計算が現代のように簡単に出来るようになったのは、インド人がゼロの発見をして、数字を現代の位取り法と言う表記にしてくれたおかげです。ピタゴラス時代の分数計算と言えばそれは複雑だったのだそうです。現在では掛け算の時には分母と分母、それに分子と分子をそれぞれかけ合わせれば答えがでます。割り算の時には分母と分子、それに分子と分母を掛け合わせると答えがでます。しかし分数計算に sin,cos,tan やルートが絡んでくるとハタと考えてしまったのです。本当に上記の分数計算は正しいのだろうか?と。
あんまり考えすぎて、マイナスと言う数字自体に疑問を持ち始めるところでした。これじゃぁピタゴラス時代の人と同じレベルです。( ^^;
ま、とにかく問題にチャレンジする時にはあまり考えすぎずに、自分の無知を知る、と言う姿勢で臨む方がいいみたいですね。
では、今日はこの辺で。
独学協友会の動画は YouTube チャンネル でご覧になれます。
閲覧(8148)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



