時空 解 さんの日記
2021
9月
22
(水)
11:20
本文
皆さんこんにちは、時空 解です。
さて、今日も朝からファインマン物理学 (以後、書籍と記す) の整理に取り掛かったのですが…
今回の節「確率 6-3 迷い歩き」のところは本当に内容が濃くて難しいです。( ^^;
まずは「迷い歩き」とはどんなものか、それを書籍から抜粋して下記に示しておきます。
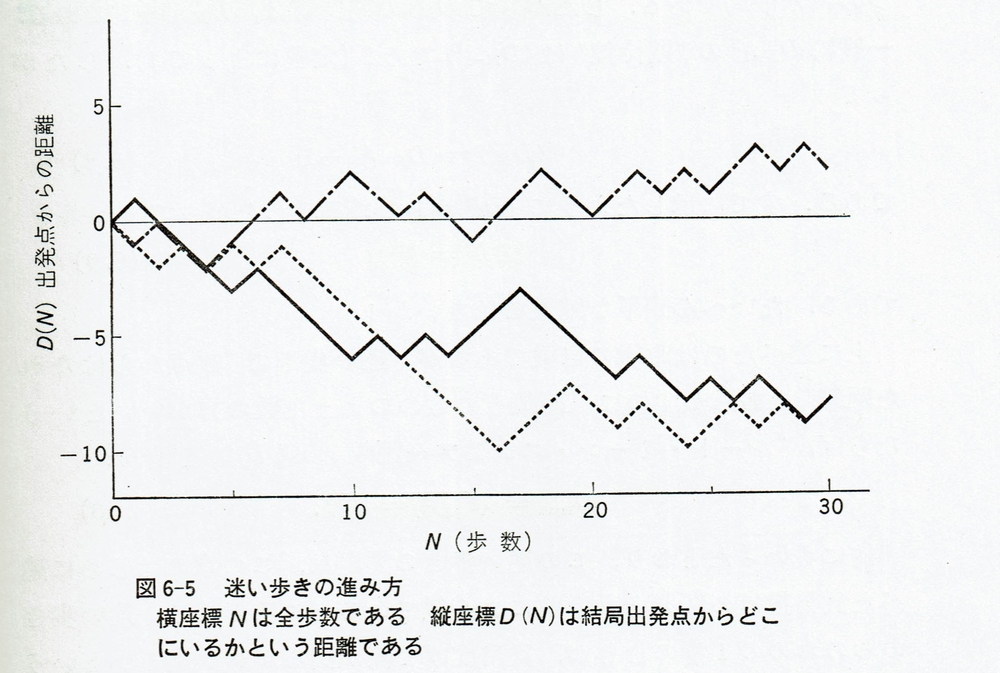
ポイントとしては下記の3つになるでしょうか。
と言うのも、書籍で行われている解説・内容自体が、私の理解を超えています。例えば下記。
うーむ…歩いた距離を絶対値で表す、と言うのには付いて行けますが、また別の測り方、自乗で進みを測ると言う考えにはいささかの疑問・躊躇を感じます。
書籍の解説には
「運動が正であっても負であっても $ D^2 $ は正であるから合理的だ…」
なんて言ってますが。(でも、この点がファインマン氏の深い洞察、そして "主観" と言っていいところかもしれません)
みなさんはこの点、どう思いますか? (私の数学力、特に確率の実力が不足しているからかも?)
まぁとにかく、そんな理由で「迷い歩き」に対する数学的なアプローチ (?) を理解することが私としては困難なんです。
(でも、これを受け入れることこそが私の Step-Up なのかも知れませんけどね)
ともかく書籍ではこのアプローチ (?) を経て、2. の「貨幣がちゃんと出来ているか否かを判別する基準 (数値)」を導き出しています。
それが下記。
$ \displaystyle \frac{ 1 }{ 2 \sqrt{ N } } $
そして実際に "貨幣投げ" による「迷い歩き」を行ったとき、上記の期待値を超えて遠くに迷い出してしまうようであれば、その貨幣は「狂っている」ことを疑える、と言っています。
でも、だからと言って
「貨幣は狂っている、と言う立証にはならない」
とも、書籍は強調しているんですよね。 …うーむ…
この「立証にはならない」、すなわち立証はできないと言うことから
「偶然的なものを実験で確かめたところで、誤差が生じるのは当たり前なのだ」
と、解説を進めます。
実験をしても誤差があることを受け入れ、そこには「主観的なもの」が含まれていることを心得ておかなくてはならない!
と、この節は戒めているようです。
いやはや、「迷い歩き」に対する数学的アプローチ (?) と言い、実験に対する戒めといい、この書籍には本当に驚かされます。
カリフォルニア理工科大学で使われていた (現在でも使われている?) 教科書と言う事を再認識させられますよね。
では今日も休日を始めています。休日の充実こそ、人生の充実です。また夜お会いできるよう、努力しています。
【今日の記事を評価して頂けましたら、下記をクリックしてね。Amazon サイトで関連書籍・商品が見れます (アフィリエイトにご協力をお願いします) 】
♪ - クリックのみでも充分に嬉しいです - ♪
------------------------------
さて、今日も朝からファインマン物理学 (以後、書籍と記す) の整理に取り掛かったのですが…
今回の節「確率 6-3 迷い歩き」のところは本当に内容が濃くて難しいです。( ^^;
まずは「迷い歩き」とはどんなものか、それを書籍から抜粋して下記に示しておきます。

この節は、上記の「迷い歩き」について数学的にアプローチ (?) をしてゆきます。迷い歩きとは
いちばん簡単にいうならば、こういう "ゲーム" である。これを "やる人" は $ x = 0 " $ の点から出発して、前 ($ +x $ の方) か後 ($ -x $ の方) かへ1歩ずつ進むという規則である。そのどちらかということの選択は、例えば貨幣を投げるというようなことによって、無作為にきめられる。この運動の結果はどうなるであろうか?
ポイントとしては下記の3つになるでしょうか。
上記の3つのポイントのうち、まず一番最初のポイントに解説を入れることが、私には出来ませんでした…_| ̄|○第6章 確率 6-3 迷い歩き
1. 彼は平均として原点から測ってどの距離にいるか?
2. 一つの貨幣が "ちゃんと" できているか、それとも "くるっているか " はどうすればわかるか? …(実は立証できない)
3. "貨幣" とか、何かそれと同じような "偶然的" なもの (例えば地面におとすと必ず上下どちらかの面が出る石) などで、表と裏との確率がちがうはずであると考える理由のあるものはどう取り扱ったらよいか?
と言うのも、書籍で行われている解説・内容自体が、私の理解を超えています。例えば下記。
「迷い歩き」において、前にいくことも後ろにいくことも全て同等に起こりやすいのだから、彼の進みは平均としてゼロであると期待せねばならぬ。しかし $ N $ (歩数) が増すにつれて、出発点から遠くにさまよい来ているという方がよりもっともらしく思われる。だから、平均として歩いた距離を絶対値であらわしたらいくらか、すなわち $ \left| D \right| $ の平均はどのくらいかということが問題になる。しかし、他の測り方をして、距離の自乗で進みを測った方がむしろ便利である:運動が正であっても負であっても $ D^2 $ は正であるから、このような迷い歩きに対しては、この測り方の方が合理的である。
うーむ…歩いた距離を絶対値で表す、と言うのには付いて行けますが、また別の測り方、自乗で進みを測ると言う考えにはいささかの疑問・躊躇を感じます。
書籍の解説には
「運動が正であっても負であっても $ D^2 $ は正であるから合理的だ…」
なんて言ってますが。(でも、この点がファインマン氏の深い洞察、そして "主観" と言っていいところかもしれません)
みなさんはこの点、どう思いますか? (私の数学力、特に確率の実力が不足しているからかも?)
まぁとにかく、そんな理由で「迷い歩き」に対する数学的なアプローチ (?) を理解することが私としては困難なんです。
(でも、これを受け入れることこそが私の Step-Up なのかも知れませんけどね)
ともかく書籍ではこのアプローチ (?) を経て、2. の「貨幣がちゃんと出来ているか否かを判別する基準 (数値)」を導き出しています。
それが下記。
$ \displaystyle \frac{ 1 }{ 2 \sqrt{ N } } $
そして実際に "貨幣投げ" による「迷い歩き」を行ったとき、上記の期待値を超えて遠くに迷い出してしまうようであれば、その貨幣は「狂っている」ことを疑える、と言っています。
でも、だからと言って
「貨幣は狂っている、と言う立証にはならない」
とも、書籍は強調しているんですよね。 …うーむ…
この「立証にはならない」、すなわち立証はできないと言うことから
「偶然的なものを実験で確かめたところで、誤差が生じるのは当たり前なのだ」
と、解説を進めます。
実験をしても誤差があることを受け入れ、そこには「主観的なもの」が含まれていることを心得ておかなくてはならない!
と、この節は戒めているようです。
いやはや、「迷い歩き」に対する数学的アプローチ (?) と言い、実験に対する戒めといい、この書籍には本当に驚かされます。
カリフォルニア理工科大学で使われていた (現在でも使われている?) 教科書と言う事を再認識させられますよね。
では今日も休日を始めています。休日の充実こそ、人生の充実です。また夜お会いできるよう、努力しています。
【今日の記事を評価して頂けましたら、下記をクリックしてね。Amazon サイトで関連書籍・商品が見れます (アフィリエイトにご協力をお願いします) 】
♪ - クリックのみでも充分に嬉しいです - ♪
------------------------------
閲覧(7763)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



