時空 解 さんの日記
2021
9月
23
(木)
10:02
本文
皆さんこんにちは、時空 解です。
今日も数学の場合の数・確率の問題に四苦八苦していました。
うーむ…こんな典型的な問題にちゃんと向き合ったことが無かったのかも知れません。

勉強不足です。_| ̄|○
四苦八苦した問題は下記のとおり。
とりあえずこの問題の答えは、右に示しておきました。ご参照くださいね。
私が
「場合の数や確率は本当に泥臭いなぁ」
と思った点は "書き並べ" や "書き出し" が必要なところがある、と言う点です。
まぁ当たり前なのかも知れませんが… ( ^^;
若い頃から数学とは
「エレガントなものだ」
と言う想いが強くある私です。
今回の 練習問題3 のように4の倍数の個数を数えるために、いわゆる "書き出し" が必要な点がどうにも面白くない・美しくない・簡素で明確でない…
そう 的確な感じがしなくて美しくない!
的確な感じがしなくて美しくない!
「数学の問題なんだから、もっとエレガントに4の倍数の個数を数えられないのか?」
と、不満に思うんです。
おっと こんな私の想いはどうでもいいですよね。m( _ _;)m すみません。
こんな私の想いはどうでもいいですよね。m( _ _;)m すみません。
とにかく4の倍数の個数が、繰り返し考えても答えと合わなかったんです。
「おかしい…?」
しばらくはどうして答えのようになるのかが分かりませんでした。
でも、使える数字が
$ 0,~1,~2,~3,~4,~5,~6 $
の7個なんですよね。
この制約があることをスッカリ忘れていた私です。これでは答えが正しく出てこないはずです。
$ 0 $ ~ $ 99 $ の間には、4の倍数が $ 100 \div 4 = 25 $ なので25個です。
でも
$ 0,~1,~2,~3,~4,~5,~6 $
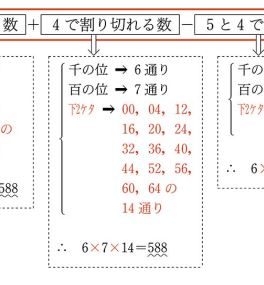
の数字しか使えないとなると、もうエレガントに個数を求めることはできないですよね? この点に付いては書籍の解答にも何も解説はありません。
14通りだと赤字で記載されているのみです。
皆さんはこの "14通り" をどのように導きますか?
私なら fx-JP900 を使って ([] はキー操作)
[0] [=] 0
[AC]
と、まずは [Ans] メモリをゼロにしておいて
[Ans] [+] [4] [=] 4 …適
[=] 8 …不適
[=] 12 …適
[=] 16 …適
[=] 20 …適
[=] 24 …適
[=] 28 …不適
・
・
・
[=] 100 …適 (これも忘れずに数える)
と、数え上げ挙げますかね?
でもこんな方法、とても泥臭いです。
「これで良いのか?数学はもっとエレガントなものだろう…」
と言う想いに心が乱れます。 (ちょっと大げさかな ( ^^; すみません)
では今日も休日を始めています。休日の充実こそ、人生の充実です。(また夜お会いできるよう、努力しています)
【今日の記事を評価して頂けましたら、下記をクリックしてね。Amazon サイトで関連書籍・商品が見れます (アフィリエイトにご協力をお願いします) 】
♪ - クリックのみでも充分に嬉しいです - ♪
------------------------------
今日も数学の場合の数・確率の問題に四苦八苦していました。
うーむ…こんな典型的な問題にちゃんと向き合ったことが無かったのかも知れません。

勉強不足です。_| ̄|○
四苦八苦した問題は下記のとおり。
「細野真宏の確率が本当によくわかる本:練習問題3」より
$ 0,~1,~2,~3,~4,~5,~6 $ の7個の数字を用いて作られる4桁の整数の
うち、5でも4でも割り切れないものはいくつあるか。
ただし、同じ数字は何回用いてもよい。
とりあえずこの問題の答えは、右に示しておきました。ご参照くださいね。
私が
「場合の数や確率は本当に泥臭いなぁ」
と思った点は "書き並べ" や "書き出し" が必要なところがある、と言う点です。
まぁ当たり前なのかも知れませんが… ( ^^;
若い頃から数学とは
「エレガントなものだ」
と言う想いが強くある私です。
今回の 練習問題3 のように4の倍数の個数を数えるために、いわゆる "書き出し" が必要な点がどうにも面白くない・美しくない・簡素で明確でない…
そう
「数学の問題なんだから、もっとエレガントに4の倍数の個数を数えられないのか?」
と、不満に思うんです。
おっと
とにかく4の倍数の個数が、繰り返し考えても答えと合わなかったんです。
「おかしい…?」
しばらくはどうして答えのようになるのかが分かりませんでした。
でも、使える数字が
$ 0,~1,~2,~3,~4,~5,~6 $
の7個なんですよね。
この制約があることをスッカリ忘れていた私です。これでは答えが正しく出てこないはずです。

$ 0 $ ~ $ 99 $ の間には、4の倍数が $ 100 \div 4 = 25 $ なので25個です。
でも
$ 0,~1,~2,~3,~4,~5,~6 $
の数字しか使えないとなると、もうエレガントに個数を求めることはできないですよね? この点に付いては書籍の解答にも何も解説はありません。
14通りだと赤字で記載されているのみです。
皆さんはこの "14通り" をどのように導きますか?
私なら fx-JP900 を使って ([] はキー操作)
[0] [=] 0
[AC]
と、まずは [Ans] メモリをゼロにしておいて
[Ans] [+] [4] [=] 4 …適
[=] 8 …不適
[=] 12 …適
[=] 16 …適
[=] 20 …適
[=] 24 …適
[=] 28 …不適
・
・
・
[=] 100 …適 (これも忘れずに数える)
と、数え上げ挙げますかね?
でもこんな方法、とても泥臭いです。
「これで良いのか?数学はもっとエレガントなものだろう…」
と言う想いに心が乱れます。 (ちょっと大げさかな ( ^^; すみません)
では今日も休日を始めています。休日の充実こそ、人生の充実です。(また夜お会いできるよう、努力しています)
【今日の記事を評価して頂けましたら、下記をクリックしてね。Amazon サイトで関連書籍・商品が見れます (アフィリエイトにご協力をお願いします) 】
♪ - クリックのみでも充分に嬉しいです - ♪
------------------------------
閲覧(8204)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



