時空 解 さんの日記
2021
10月
17
(日)
09:36
本文
皆さんこんにちは、時空 解です。
今日は昨日につづいて練習問題17について書いてみます。
まずは問題文から

この問題の解説と答は右画像に示すことにします。
この解答をみて、みなさんはどんな印象を持ちましたか…?
私などは
「整数 $ x,~y,~z $ の組」
と言う1文から、記述式の解答の中に $ \displaystyle \frac{ 1 }{ 2 } $ がでてくること自体、違和感を感じます。
直感的に
「こんな解答は間違えている」
と、頭が考えてしまうんですよね。
でも、この問題は $ \displaystyle \frac{ 1 }{ 2 } $ をどう扱うのかが最大のポイントだし、オリジナリティとも言えます。
よくよく考えてみると、面白い。
そう言えば、この $ \displaystyle \frac{ 1 }{ 2 } $ を見て リーマン予想 を連想する方はいらっしゃいますか?
(ちょっと飛躍しすぎかもしれませんが…( ^^; )
リーマンは半整数を使って、素数の個数を導こうとしたんですよね。確か…
(半整数と言うのは、れっきとした数学用語のようです)
まぁリーマン予想・素数の個数 に付いては横に置いておいて…
ともかく練習問題17のように、整数に限定された値を扱っている中で分数を含む記述をするところが、私に取ってはとても斬新でした。
練習問題17を解くために、例えば $ n = 0 $ とか $ n = 1 $ の場合の $ x,~y,~z $ の組を書き並べてみたりしますよね。
(昨日のコメントで、会員の方が実際に書き並べて下さっています)
昨日、私も書き並べてみたのですが、会員の方と同様に
$ n = 0 $ の時 $ ( x,~y,~z) = (0,~0,~0) $
$ n = 1 $ の時 $ ( x,~y,~z) = (2,~0,~0),~ (0,~1,~0),~ (0,~0,~1) $
としました。
でも違うんですよね。
練習問題17の解答・解説を理解してから、改めて考えてみて、下記のようになることに気が付きました。
$ n = 0 $ の時 $ ( x,~y,~z) = (0,~0,~0) $
$ n = 1 $ の時 $ ( x,~y,~z) = \textcolor{red}{ (1,~0,~0) },~ (2,~0,~0),~ (0,~1,~0),~ (0,~0,~1) $
赤で示した整数 $ x,~y,~z $ の組を見落す私です…。_| ̄|○
$ \displaystyle \frac{ x }{ 2 } $ の $ x $ に $ 1 $ を入れると $ \displaystyle \frac{ 1 }{ 2 } $ になるので、なんとなく整数ではない気がしてしまいます。勝手に頭のなかで $ \displaystyle \frac{ 1 }{ 2 } $ のイメージが走ってしまう。
でも、あくまでも $ x $ に $ 1 $ を代入しているだけで、$ x $ は $ 1 $ なんです。整数なんですよね。
「細野真宏の確率が本当によくわかる本」の解答の解説の中にでてくる「注1、注2」がとても重要なポイントです。
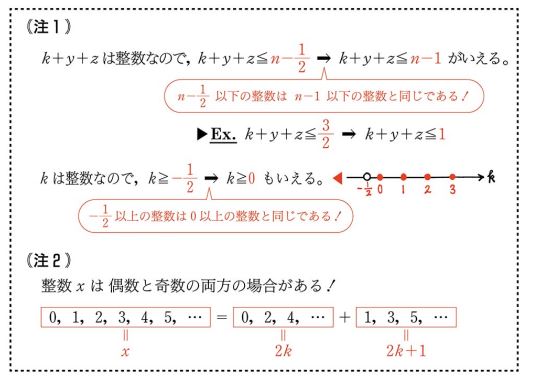
偶数と奇数とを場合分けする必要がある。と、気が付くところもポイントでしょうか。
数学検定の1級で出題される問題って、練習問題17のような問題なのかなぁ…と思うのは私だけかな…? ( ^^;
では今日も休日を始めています。休日の充実こそ、人生の充実です。また夜お会いできるよう、努力しています。
【今日の記事を評価して頂けましたら、下記をクリックしてね。Amazon サイトで関連書籍・商品が見れます (アフィリエイトにご協力をお願いします) 】
♪ - クリックのみでも充分に嬉しいです - ♪
------------------------------
今日は昨日につづいて練習問題17について書いてみます。
まずは問題文から
練習問題17
$ n $ を $ 0 $ 以上の整数とし、$ \displaystyle \frac{ x }{ 2 } + y + z \leqq n,~~x \geqq 0,~~y \geqq 0,~~z \geqq 0 $ を満たす
整数 $ x,~y,~z $ の組 $ (x,~y,~z) $ の個数を求めよ。

この問題の解説と答は右画像に示すことにします。
この解答をみて、みなさんはどんな印象を持ちましたか…?
私などは
「整数 $ x,~y,~z $ の組」
と言う1文から、記述式の解答の中に $ \displaystyle \frac{ 1 }{ 2 } $ がでてくること自体、違和感を感じます。
直感的に
「こんな解答は間違えている」
と、頭が考えてしまうんですよね。
でも、この問題は $ \displaystyle \frac{ 1 }{ 2 } $ をどう扱うのかが最大のポイントだし、オリジナリティとも言えます。
よくよく考えてみると、面白い。
そう言えば、この $ \displaystyle \frac{ 1 }{ 2 } $ を見て リーマン予想 を連想する方はいらっしゃいますか?
(ちょっと飛躍しすぎかもしれませんが…( ^^; )
リーマンは半整数を使って、素数の個数を導こうとしたんですよね。確か…
(半整数と言うのは、れっきとした数学用語のようです)
まぁリーマン予想・素数の個数 に付いては横に置いておいて…
ともかく練習問題17のように、整数に限定された値を扱っている中で分数を含む記述をするところが、私に取ってはとても斬新でした。
練習問題17を解くために、例えば $ n = 0 $ とか $ n = 1 $ の場合の $ x,~y,~z $ の組を書き並べてみたりしますよね。
(昨日のコメントで、会員の方が実際に書き並べて下さっています)
昨日、私も書き並べてみたのですが、会員の方と同様に
$ n = 0 $ の時 $ ( x,~y,~z) = (0,~0,~0) $
$ n = 1 $ の時 $ ( x,~y,~z) = (2,~0,~0),~ (0,~1,~0),~ (0,~0,~1) $
としました。
でも違うんですよね。
練習問題17の解答・解説を理解してから、改めて考えてみて、下記のようになることに気が付きました。
$ n = 0 $ の時 $ ( x,~y,~z) = (0,~0,~0) $
$ n = 1 $ の時 $ ( x,~y,~z) = \textcolor{red}{ (1,~0,~0) },~ (2,~0,~0),~ (0,~1,~0),~ (0,~0,~1) $
赤で示した整数 $ x,~y,~z $ の組を見落す私です…。_| ̄|○
$ \displaystyle \frac{ x }{ 2 } $ の $ x $ に $ 1 $ を入れると $ \displaystyle \frac{ 1 }{ 2 } $ になるので、なんとなく整数ではない気がしてしまいます。勝手に頭のなかで $ \displaystyle \frac{ 1 }{ 2 } $ のイメージが走ってしまう。
でも、あくまでも $ x $ に $ 1 $ を代入しているだけで、$ x $ は $ 1 $ なんです。整数なんですよね。
「細野真宏の確率が本当によくわかる本」の解答の解説の中にでてくる「注1、注2」がとても重要なポイントです。

偶数と奇数とを場合分けする必要がある。と、気が付くところもポイントでしょうか。
数学検定の1級で出題される問題って、練習問題17のような問題なのかなぁ…と思うのは私だけかな…? ( ^^;
では今日も休日を始めています。休日の充実こそ、人生の充実です。また夜お会いできるよう、努力しています。
【今日の記事を評価して頂けましたら、下記をクリックしてね。Amazon サイトで関連書籍・商品が見れます (アフィリエイトにご協力をお願いします) 】
♪ - クリックのみでも充分に嬉しいです - ♪
------------------------------
閲覧(7394)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



