時空 解 さんの日記
2021
10月
31
(日)
09:47
本文
皆さんこんにちは、時空 解です。
今日は数学検定の日。朝から復習をしている次第です。
さて、現在進行形で「実用数学技能検定要点整理 2級」を復習しているところなんですが、今、ブログネタにできそうな注意点に遭遇しました。
今日はこれに付いて書いてみたいと思います。
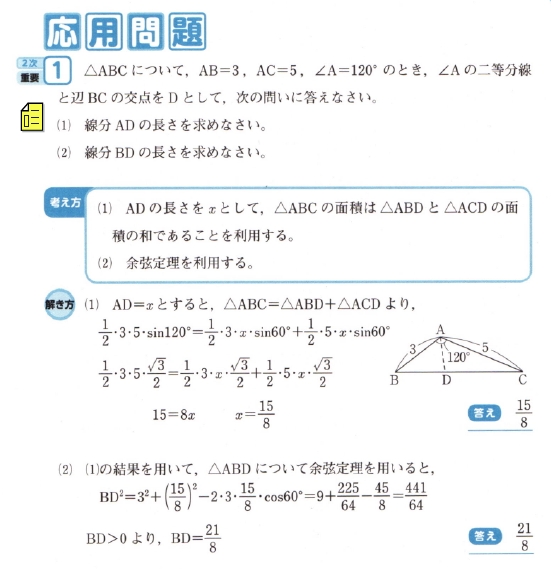
注意した方がいい点がある問題は、表題にも書きましたが p71 の 応用問題1です。
問題とその解答は右画像にゆだねるとして、さて、この問題、ちょっとした疑問を感じたりはしませんか?
どうして (1) と (2) の解法で、(1) は面積を利用して (2) は余弦定理なんだろう?
とね。
(1) も余弦定理を利用して解けそうな気がしますよね。
実際にやろうとした方も多いのではないでしょうか?
でもやってみると、間違った答えが出てくるんです。
そうではなく、
「あ、これはルートを含む複雑な計算式になるからダメだな」
と、判断できたのなら、それはそれで大丈夫です。これでしたら面積を利用する解法へと、思考回路を変更できるでしょう。
でも、私のように、余弦定理を利用した式を立てる段階で、ルートを含むことはないと思ってしまうと失敗します。( ^^;
私がやってしまった失敗は下記のとおり…。
(1) に余弦定理を利用して式を立てると、下記のようになります。
線分 $ BC $ の長さは線分 $ BD + DC $ なのだから、求めたい線分 $ AD $ の長さを $ x $ とすると
$ BC^2 = AB^2 + AC^2 -2 \cdot AB \cdot AC \cdot \cos 60^\circ = 49 $
$ BD^2 = AB^2 + x^2 -2 \cdot AB \cdot x \cdot \cos 60^\circ = 3^2 + x^2 -2 \cdot 3 \cdot x \cdot \displaystyle \frac{ 1 }{ 2 } $
$ DC^2 = x^2 + AC^2 -2 \cdot x \cdot AC \cdot \cos 60^\circ = x^2 + 5^2 -2 \cdot x \cdot 5 \cdot \displaystyle \frac{ 1 }{ 2 } $
$ BD + DC = BC $ なのだから $ BD^2 + DC^2 = BC^2 $ より (これが私の勘違いなんですけどね)
$ \left( 3^2 + x^2 -2 \cdot 3 \cdot x \cdot \displaystyle \frac{ 1 }{ 2 } \right) + \left( x^2 + 5^2 -2 \cdot x \cdot 5 \cdot \displaystyle \frac{ 1 }{ 2 } \right) = 49 $
$ x $ について上記を解くと $ AD $ の値は $ \displaystyle \frac{ 4 + \sqrt{ 46 } }{ 2 } $ なんて数値か出てきてしまいます。
始めはどうして間違った数値が出てくるのか、納得が出来ませんでした。でも簡単な例を挙げてみて、やっと納得できました。( ^^;
$ 1 + 3 = 4 $ ですよね。
ですが
$ 1^2 = 1 $
$ 3^2 = 9 $
従って
$ 1^2 + 3^2 = 10 $
$ 4^2 = 16 $
だから
$ 1^2 + 3^2 \neq 4^2 $
自分の直感に振り回されている自分に気が付いた今日でした‥‥ _| ̄|○
さて、落ち込んでなんで次に進みます。
では今日も休日を始めています。休日の充実こそ、人生の充実です。また夜お会いできるよう、努力しています。
【今日の記事を評価して頂けましたら、下記をクリックしてね。Amazon サイトで関連書籍・商品が見れます (アフィリエイトにご協力をお願いします) 】
♪ - クリックのみでも充分に嬉しいです - ♪
------------------------------
今日は数学検定の日。朝から復習をしている次第です。
さて、現在進行形で「実用数学技能検定要点整理 2級」を復習しているところなんですが、今、ブログネタにできそうな注意点に遭遇しました。
今日はこれに付いて書いてみたいと思います。

注意した方がいい点がある問題は、表題にも書きましたが p71 の 応用問題1です。
問題とその解答は右画像にゆだねるとして、さて、この問題、ちょっとした疑問を感じたりはしませんか?
どうして (1) と (2) の解法で、(1) は面積を利用して (2) は余弦定理なんだろう?
とね。
(1) も余弦定理を利用して解けそうな気がしますよね。
実際にやろうとした方も多いのではないでしょうか?
でもやってみると、間違った答えが出てくるんです。
そうではなく、
「あ、これはルートを含む複雑な計算式になるからダメだな」
と、判断できたのなら、それはそれで大丈夫です。これでしたら面積を利用する解法へと、思考回路を変更できるでしょう。
でも、私のように、余弦定理を利用した式を立てる段階で、ルートを含むことはないと思ってしまうと失敗します。( ^^;
私がやってしまった失敗は下記のとおり…。
(1) に余弦定理を利用して式を立てると、下記のようになります。
線分 $ BC $ の長さは線分 $ BD + DC $ なのだから、求めたい線分 $ AD $ の長さを $ x $ とすると
$ BC^2 = AB^2 + AC^2 -2 \cdot AB \cdot AC \cdot \cos 60^\circ = 49 $
$ BD^2 = AB^2 + x^2 -2 \cdot AB \cdot x \cdot \cos 60^\circ = 3^2 + x^2 -2 \cdot 3 \cdot x \cdot \displaystyle \frac{ 1 }{ 2 } $
$ DC^2 = x^2 + AC^2 -2 \cdot x \cdot AC \cdot \cos 60^\circ = x^2 + 5^2 -2 \cdot x \cdot 5 \cdot \displaystyle \frac{ 1 }{ 2 } $
$ BD + DC = BC $ なのだから $ BD^2 + DC^2 = BC^2 $ より (これが私の勘違いなんですけどね)
$ \left( 3^2 + x^2 -2 \cdot 3 \cdot x \cdot \displaystyle \frac{ 1 }{ 2 } \right) + \left( x^2 + 5^2 -2 \cdot x \cdot 5 \cdot \displaystyle \frac{ 1 }{ 2 } \right) = 49 $
$ x $ について上記を解くと $ AD $ の値は $ \displaystyle \frac{ 4 + \sqrt{ 46 } }{ 2 } $ なんて数値か出てきてしまいます。
始めはどうして間違った数値が出てくるのか、納得が出来ませんでした。でも簡単な例を挙げてみて、やっと納得できました。( ^^;
$ 1 + 3 = 4 $ ですよね。
ですが
$ 1^2 = 1 $
$ 3^2 = 9 $
従って
$ 1^2 + 3^2 = 10 $
$ 4^2 = 16 $
だから
$ 1^2 + 3^2 \neq 4^2 $
自分の直感に振り回されている自分に気が付いた今日でした‥‥ _| ̄|○
さて、落ち込んでなんで次に進みます。
では今日も休日を始めています。休日の充実こそ、人生の充実です。また夜お会いできるよう、努力しています。
【今日の記事を評価して頂けましたら、下記をクリックしてね。Amazon サイトで関連書籍・商品が見れます (アフィリエイトにご協力をお願いします) 】
♪ - クリックのみでも充分に嬉しいです - ♪
------------------------------
閲覧(7821)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



