皆さんこんにちは、時空 解です。

今日は "7-4 ニュートンの引力の法則" の整理が途中でしたので、その続きを再開します。
あまりにも有名で、もう当たり前の引力の法則ですが、ファインマン物理学書はここをどのように解説するのか？この点が面白いところです。

"月が地球に向かって落ちる" と考えて
「では、地球上で物が落ちるのも月の落ち方も同じ何か？」
と考えを進め検証して行く辺りが、既成概念に囚われずに理論を展開できるお手本のようですね。

 

第７章　万有引力の理論 7-4 ニュートンの引力の法則

・ニュートンは、惑星が同じ時間の間に同じ面積をおおうというそのことこそ、直線方向からのはずれが半径方向であるということのあらわれであって、- 面積の法則は、すべての力がまさに太陽の方にむかっているという考えから直接出てくることを証明した。
・ケプラーの第３法則をよくしらべると、惑星が遠ければ遠いほど力が弱いいうことがでてくる。(中略) 距離の自乗に逆比例することがわかる。

上の二つの法則を組み合わせて、ニュートンは、距離の自乗に反比例した力が二つの物体を結ぶ直線にそってはたらいているに相違ないという結論に達したのである。

・次の問題は、地球がその上にいる人間を引く力も、地球が月を引く力と "同じ" ように、距離の自乗に反比例するものであるかどうかということであった。

月は、力がはたらいていなかったとした場合にあるべき場所から、実は落ちているのである。月の軌道の半径 (およそ240,000マイル) と、地球のまわりを１回まわるのにようする時間 (およそ 29日) とはわかっているから、月が１秒間に軌道の上を動く距離は、それから求められる。また１秒間に月がどのくらい落ちるかを計算することもできる。この距離を求めると、１秒間に $ \displaystyle \frac{ 1 }{ 20 } $ インチとなる。ところで地球の半径は 4000 マイルであって、地球の中心から 4000 マイルのところ、すなわち地表では物体は１秒間に 16 フィート落ちる。したがって月のある 240,000マイルのところ、すなわち地球の半径の 60倍もの遠いところては 16フィートの $ \displaystyle \frac{ 1 }{ 3600 } $ だけしか落ちないわけで、16フィートの $ \displaystyle \frac{ 1 }{ 3600 } $ はまさに１インチの $ \displaystyle \frac{ 1 }{ 20 } $ である。

・このように逆自乗の法則に実によくあうのである。
(ここまでが前回整理した部分)

・月が "落ちてくる" といっても、月が我々に近よってくるわけではないのだから、この考えはいささか分かりにくい。しかしこれはいい考え方であるから、もう少し説明を加えておこう。

月が落ちるという意味は、もしも力がなかったらそれにそって進むであろう直線からはずれ落ちるということなのである。
地球の表面近くで物体を放すと、最初の１秒間には16フィート落ちる。水平に打ち出されたものも、16フィート落ちる。水平方向にも動いているのだけれども、最初の１秒間に落ちる距離はやはり16フィートである。図 7-3 はこのことを示す仕掛けである。途が水平になっているところにタマがあって、その先からまさに飛び出そうとしているところである。それと同じ高さのところに別のタマがあって、これはま下に落ちる。そして、スイッチがあって、第１のタマがその途を離れる瞬間に、第２のタマが落ちはじめるようになっている。この二つのタマは空中で衝突する。このことは、同じ時刻には二つのタマが同じ高さにいるということの証拠になる。

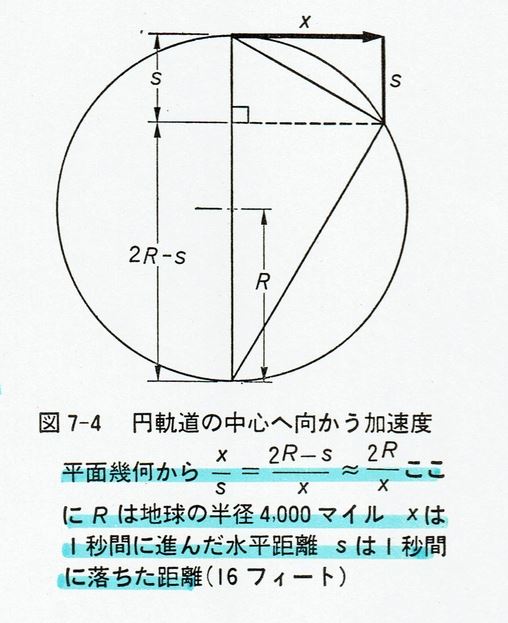
小銃弾などを水平にねらいをつけて打ち出したとすると、それは１秒間に遠くへ - 2000フィートくらい - 飛んでいくが、それでもやはり16フィートは落ちる。それでは小銃弾の速さをだんだん大きくしていったらどういうことになるか？　ここで、地球の表面に曲率があることを忘れてはならない。弾の速さが充分大きいと、16フィート落ちても、地面からの高さが前とちょうど同じだということがありうるわけである。それはどういうときか？弾は落ちる、けれども地球は曲がって遠ざかるので、弾は地球の "まわり" に落ちるのである。だから、問題は、地球が水平から16フィート下にあるようにするためには、弾は１秒間にどこまでいっていなければならないか、ということになる。図 7-4 に示したとおり、地球の半径は4000マイルであって、接線はもしも力がなかったとしたら弾が進むであろう途を示している。ここで次のような平面幾何のきれいな定理を使う。それは、この接線に平行な弦をひいて、直径を２分すると、接線の長さは、この二つの部分の長さの比例中項に等しい、という定理である。この定理を使うと、弾の進む水平距離は、落下距離16フィートと、地球の直径8000マイルとの比例中項であることになる。$ \displaystyle \frac{ 16 }{ 5280 } × 8000 $ の平方根は、ほとんど５マイルである。だから、弾の速さが１秒に５マイルであるならば、毎秒16フィートという一定の割合で地面に向かって落ちつづける。しかし地面もそれだけ曲がって退くので、弾は決して地面に近付くことはない。

さて、今日はここまでにしておきます。重要なところは本文をそのまま丸写しにしてありますが、分かり難いところもあります。平面幾何のきれいな定理…比例中項から５マイルを導き出すところが個人的には分かり難くかったです。

ファインマン物理学のここの部分 (小銃弾のところ) を若き頃読んだのですが、５マイルをどう計算で導き出すのか分かりませんでした。…まぁいつものように鉛筆を取り出して、実際に数式を書いて行かなかったので分からないままだったのですけどね。
今日は具体的にやってみました。

小銃弾の弾が１秒間にどれくらい水平方向に飛べばよいのか？その飛距離を $ x $ としているのですよね。引力で地面の落ちる距離は $ s $ であって、これが $ 16 $ フィート。この $ 16 $ の単位をフィートからマイルに変換する必要がありますので、
$ \displaystyle \frac{ 16 }{ 5280 } = \frac{ 1 }{ 330 } $　　　( １マイルは約５２８０フィート )

となります。
地球の半径が $ R $ で、これは $ 4000 $ マイルです。図 7-4 の計算式　$ \displaystyle \frac{ x }{ s } = \frac{ 2R - s }{ x } $　に数値を代入すると

$ \displaystyle \frac{ x }{ \frac{ 1 }{ 330 } } = \frac{ 2 \cdot 4000 - \frac{ 1 }{ 330 } }{ x } $

となります。$ x $ について整理すると

$ x^2 = 8000 \cdot \displaystyle \frac{ 1 }{ 330 } - ( \frac{ 1 }{ 330 } )^2 $


となり $ x $ が求められます。

まだ比例中項と言う平面幾何のところが自分としては学習不足ですが、とりあえず２０代の前半の時よりも理解は進みました。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。