時空 解 さんの日記
2022
6月
30
(木)
09:27
本文
皆さんこんにちは、時空 解です。
絶対値記号と言うものにそれなりに注意をしてきたのですが、まだまだ注意が必要だと認識しています。
例えば、下記の等式について、変数と $ x $ が $ 5 $ の時、定数 $ a $ はどんな数値を取ると思いますか?
$ a = x - 3 $
これは簡単ですよね。$ x = 5 $ なのですから代入すると、$ a = 2 $ と出て来ます。
では次に絶対値記号が入ってくるとどうなるのでしょうか?
$ a = \left| x - 3 \right| $
これも分からない訳ではありませよね。$ x = 5 $ なので同じように代入して、$ a = 2 $ を得ます。
でも、今度は $ a = 2 $ となるような $ x $ の値は? と言う問いになるとちょっと難しくなってきますよね。
下記の等式において、$ a = 2 $ となるような $ x $ の値を求めよ。
$ a = x - 3 $
これは簡単。$ x = 5 $ ですよね。では続いて次の問題はどうでしょうか?
下記の等式において、$ a = 2 $ となるような $ x $ の値を求めよ。
$ a = \left| x - 3 \right| $
この解答に戸惑う私です… ( ^^;
答えは分かりますよね。$ x = 5 $ と、それから $ x = 1 $ も答えですね。
でも、この問題を記述式で解答をするとなると、どう記述すればよいのでしょうか?
絶対値記号を外す数式を記述する習慣も身に付けていないと、いざと言う時に答えられません。
記述するのに戸惑ったり、もう一つの答えが抜けてしまったりすることを認識しました。
下記の等式において、$ a = 2 $ となるような $ x $ の値を求めよ。
$ a = \left| x - 3 \right| $
上記のような単純な問題でも、いざ記述しろと言われても記述出来なかった私です。
$ a = \left| x - 3 \right| $
$ \pm a = x - 3 $
両辺に $ 3 $ を加えると
$ 3 \pm a = x $
したがって $ x $ は $ 5,~1 $
今日の朝、やっと上記のような記述ができるようになった私です。
ついでにグラフも書いておきましょう。
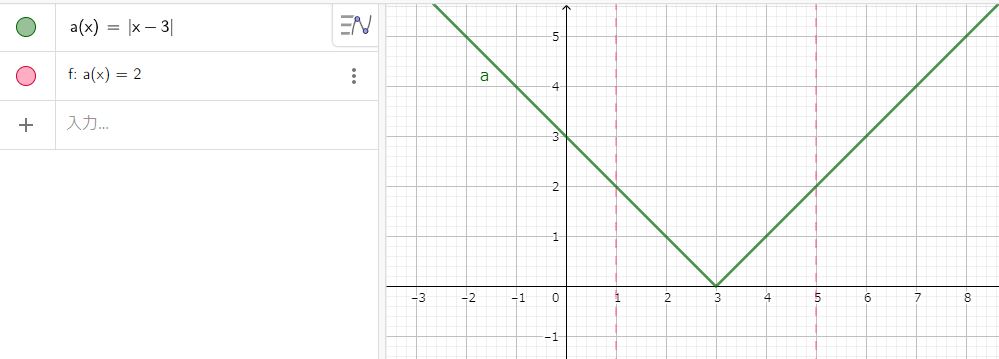
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
絶対値記号と言うものにそれなりに注意をしてきたのですが、まだまだ注意が必要だと認識しています。
例えば、下記の等式について、変数と $ x $ が $ 5 $ の時、定数 $ a $ はどんな数値を取ると思いますか?
$ a = x - 3 $
これは簡単ですよね。$ x = 5 $ なのですから代入すると、$ a = 2 $ と出て来ます。
では次に絶対値記号が入ってくるとどうなるのでしょうか?
$ a = \left| x - 3 \right| $
これも分からない訳ではありませよね。$ x = 5 $ なので同じように代入して、$ a = 2 $ を得ます。
でも、今度は $ a = 2 $ となるような $ x $ の値は? と言う問いになるとちょっと難しくなってきますよね。
下記の等式において、$ a = 2 $ となるような $ x $ の値を求めよ。
$ a = x - 3 $
これは簡単。$ x = 5 $ ですよね。では続いて次の問題はどうでしょうか?
下記の等式において、$ a = 2 $ となるような $ x $ の値を求めよ。
$ a = \left| x - 3 \right| $
この解答に戸惑う私です… ( ^^;
答えは分かりますよね。$ x = 5 $ と、それから $ x = 1 $ も答えですね。
でも、この問題を記述式で解答をするとなると、どう記述すればよいのでしょうか?
絶対値記号を外す数式を記述する習慣も身に付けていないと、いざと言う時に答えられません。
記述するのに戸惑ったり、もう一つの答えが抜けてしまったりすることを認識しました。
下記の等式において、$ a = 2 $ となるような $ x $ の値を求めよ。
$ a = \left| x - 3 \right| $
上記のような単純な問題でも、いざ記述しろと言われても記述出来なかった私です。
$ a = \left| x - 3 \right| $
$ \pm a = x - 3 $
両辺に $ 3 $ を加えると
$ 3 \pm a = x $
したがって $ x $ は $ 5,~1 $
今日の朝、やっと上記のような記述ができるようになった私です。
ついでにグラフも書いておきましょう。

では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(7720)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



