皆さんこんにちは、時空 解です。

絶対値記号が付いている方程式の解法になかなか慣れていない自分に気が付きました。
表題にも書きましたが、

$ \left| x \right| = 1 $ の変数 $ x $ の値は？

と言う問題があったとすると、この答えは $ 1 $ または $ -1 $ ですよね。
これほどにシンプルな数式であれば、答えが２個あることにもあまり抵抗は感じません。

でも、例えば下記のような数式だったとしましょう。

$ \left| x-4 \right| \lt 2 \sqrt{ 5 } $

こうなった場合、もう $ x $ の値が具体的にどうなるのか五里霧中の私でした。特に不等号が出てくるとね、難しく感じますよね。

これが例えば下記のように等号の方程式だったら

$ \left| x-4 \right| = 2 \sqrt{ 5 } $

答えは見えてきます。答えは絶対値記号をまず外して

$ x-4 = \pm 2 \sqrt{ 5 } $

と出来ますから

$ x = 4 \pm 2 \sqrt{ 5 } $

と変形して、$ x $ の値は $ 4 -2 \sqrt{ 5 } $ または $ 4 + 2 \sqrt{ 5 } $ となります。


さて、等号の式を解いた後なら、先ほどの不等号の式の答えも見えてきますね。

$ \left| x-4 \right| \lt 2 \sqrt{ 5 } $
上式は

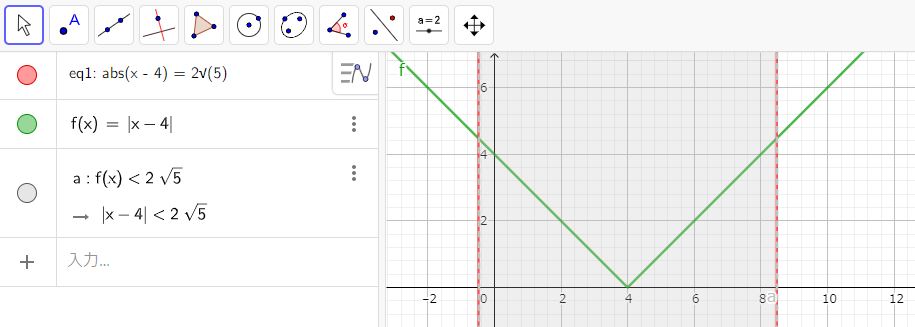
$ 4 -2 \sqrt{ 5 } \lt x \lt 4 + 2 \sqrt{ 5 } $

と、$ x $ の取り得る値の範囲を示すことができます。

数学の問題を解いていると、圧倒的に等号による方程式を扱うほうが多いので、方程式を解くと大抵が、答えは一つです。
２次方程式なら２つですけどね。この理由は、例えば
$ x^2 = 1 $
と言う等式の場合もそうですが、$ x $ はプラスとマイナスの値の両方が取れるからでよね。

絶対値記号が含まれる等式も、慣れてくると答えが２つ出てくると言うのが当たり前になりますが、慣れてないとね。

１次の等式だと、絶対値記号を含んでいたとしても、答えが２つ出てくるとね。 (プラス値とマイナス値)
何だか変な気がするのは私だけでしょうか？

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )