皆さんこんにちは、時空 解です。

今日は専門学校を卒業して、単身、就職のために神奈川県で独り暮らしを始めた頃に抱いていた疑問について書いてみたいと思います。

その疑問と言うのは
「$ y = x $ と $ f(x) = x $ って、根本的にどう違うんだろうなぁ…」
と言うものです。

当時「スミルノフの高等数学教程」と言う、全１２巻からなる書籍を手にしていました。物理学者になるための必読の数学書として、専門学校時代に先生に進められたことがあったからです。


当時はうぬぼれ屋でしたので、やる気さえ出せば「スミルノフの高等数学教程」を学習することが出来ると信じていたんです。
それで、第１巻をぼちぼちと勉強し始めた頃でした。

そんな頃です。書籍の解説を読むと…
「これを $ f(x) $ とすると…」
と言うやり方が目につくようになったんです。

当時の私はどうして数式を $ f(x) $ と置いて良いのか？　または $ f(x) $ と置くのか？　そんな疑問にさいなまれてシックリ行かなかったんです。

中学のときに学ぶ数学では、始めにグラフ有りきで、そこに $ x $ 軸と $ y $ 軸と言うのが前提として有りましたよね。
ですから、$ x $ と $ y $ との関係式 $ y = x $ は何の疑問も持たずにグラフ化も出来ました。

でも、前提が無いのに、下記のような解説が出てくるとどうしても頭の中に疑問が生じたんです。( ^^;
「$ x $ を $ f(x) $ と表して…」
勝手においていいのか！　…なんてね。

数式を $ f(x) $ とする、って、数学的なイメージもしますよね。それでとても気になったんです。
でも、$ y = x $ の $ y $ との違いが分からなくてね。

これが、当時の自分が気持ちよく数学の学習を進められなかった理由の１つでもあるんです。
でも、これがやっと最近解消されました。
想えば「スミルノフの高等数学教程」なんかを手にするのが早かったというだけのことでした。

まずは高校数学の参考書「チャート式数学」を学習しないとね。(まぁそんなことはともかく)


さて、最近 $ y = x $ と $ f(x) = x $ の違い・使い分けが自分の中で明確にできるようになりました。

まぁ $ y = x $ と言うのは $ f(x) = x $ の代表的な数式の１つとも言えます。
つまり $ y = x $ と言うのは、先にも書きましたが前提として、

$ x $ 軸と $ y $ 軸が用意されている状況

だからこその数式なんです。
でも、$ f(x) $ と言うのは、$ x $ に伴って変化する「とある物」を表している記号なんです。
この「とある物」をグラフにしようとした場合、縦軸に $ f(x) $ を取ってグラフを描くんですよね。

具体例を挙げてみましょう。数直線を始めに想定します。

数直線上に、点 $ A $ と点 $ B $ があります。点 $ A $ は $ -2 $ の所。点 $ B $ は $ 1 $ のところです。
$ AB $ を $ 3:2 $ に内分する点 $ P $ は、数直線上のどの位置にくるでしょう？

上記のような問題が有ったとしますよね。この問題を解くために $ f(x) $ とか $ g(x) $ を、自ら想定して (ここが始めから用意されている $ y $ とは違う点) 何にするのかを考えて問題を解くんです。
繰り返しますが、自ら「とある物」を選んで $ f(x) $ とか $ g(x) $ に対応させて考えるんです。

点 $ P $ は当然数直線上に乗っかるので、数直線を $ x $ 軸と捉えても差し支えありません。
さて、$ AB $ を $ 3:2 $ に内分する点 $ P $ の位置を $ x $ としましょう。そうすると $ AP : PB = 3 : 2 $ と言う等式が成り立つのは分かりますよね。

$ AP = \left| x-(-2) \right| $
$ PA = \left| 1-x \right| $

ですから、 $ AP : PB = 3 : 2 $ より
$ 2 \left| x-(-2) \right| = 3 \left| 1-x \right| $

が成立します。上記の式を解けば内分点の位置 $ x $ が分かります。でも、この上式は絶対値が含まれていてちょっとピンのきません。
こんな時に、例えば左辺と右辺をそれぞれ置き換えてみるんです。

左辺：$ f(x) = 2 \left| x-(-2) \right| $
右辺：$ g(x) = 3 \left| 1-x \right| $

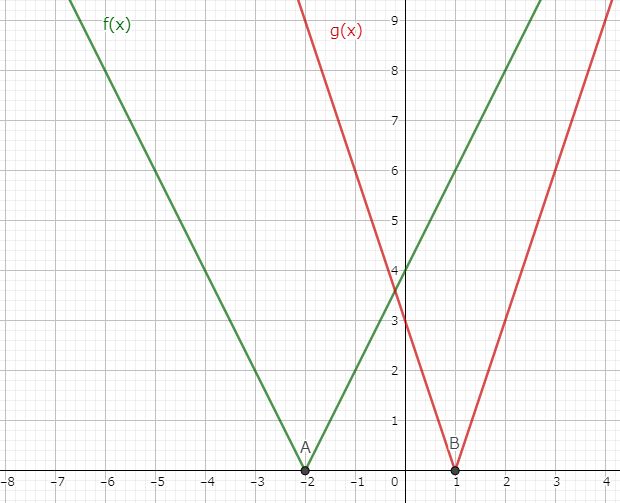
こうすると、$ x $ の値は $ f(x) $ と $ g(x) $ の交点だということも見えてきますよね。
この２つの関数 $ f(x) $ と $ g(x) $ をグラフに描いてみました。これで交点が見えましたね。

こんな風に、$ f(x) $ と言う記号は利用して行くんですよね。 $ y $ と $ f(x) $ の違い、私はこんな風にイメージしています。
皆さんはどんな風に捉えていますか？

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )