時空 解 さんの日記
2022
8月
8
(月)
09:40
本文
皆さんこんにちは、時空 解です。
8月5日に内分点の問題を例に「$ y=x $ の $ y $」と「$ f(x)=x $ の $ f(x) $」との違いについて書いてみました。
今日はこの問題を利用して、数直線上の値と、絶対値記号の関係について考えて行こうと思います。

まずは8月5日に取り上げた問題を書いておきます。
一般に数直線上の2点 $ A,~B $ に対して $ m : n $ に内分する点外分する点の位置 $ x $ を計算するには、公式がありますよね。
下記に示してみますと…
内分点は $ x = \displaystyle \frac{ na + mb }{ m + n } $
外分点は $ x = \displaystyle \frac{ -na + mb }{ m - n } $
となります。(右画像参照)
さて、この公式を覚えることは簡単です。
それに内分点を求めるには $ AP : PB = (x-a) : (b-x) = m : n $ の式から、その公式を導くことも出来ますよね。大したことではないでしょう。
でもこの公式、内分点と外分点の関係がどうして $ n $ の $ \cancel{ \mp } $ プラス・マイナス (2022-08-10 修正) に関係してくるのか、ちゃんと説明しようとすると言葉を失ったりしますよね。
なかなか難しいです。
そもそも内分点と言うのは分かりますが、外分点と言うのはどんな理由から存在している点なんでしょうかね?内分点と外分点、それと $ n $ と $ -n $ の関係とはどんなものなんでしょうか?
これは、結論から言いますと絶対値記号を使うと場合分けが必要になることに関係があります。
絶対値記号を外す時には、内部がマイナス値かプラス値かで場合分けをする必要がありますよね。内部がマイナス値だった場合は、全体をマイナス記号で括らなくてはなりません。
例) $ \left| x + 2 \right| $
・$ -2 \leqq x $ の場合
$ (x + 2) $
・$ x \lt -2 $ の場合
$ -(x + 2) $
でも、この場合分けと内分点・外分点は残念ながら「直接対応」はしていません。
関係はあるんですけどね。 (2022-08-11 修正)
絶対値記号を外す時の場合分けと、内分点・外分点の違いを表す $ n,~-n $ がどう対応しているのか?
それが分かると、公式も気持ちよく利用できるようになるんですけどね。私は高校時代から今まで、気持ちよく利用できていなかったんです。( ^^;
でもやっと、理解できました。 する為の方向性が見えてきました。(2022-08-11 修正・追記)
そのきっかけは、先に示した問題の内分点を、fx-JP900 のソルブ機能を使って答えを計算したことにあります。
$ AB $ を $ 3:2 $ に内分する点 $ P $ の数直線上の値を $ x $ とすると下記の数式が成立するはずです。
$ AP:PB = 3:2 $ より
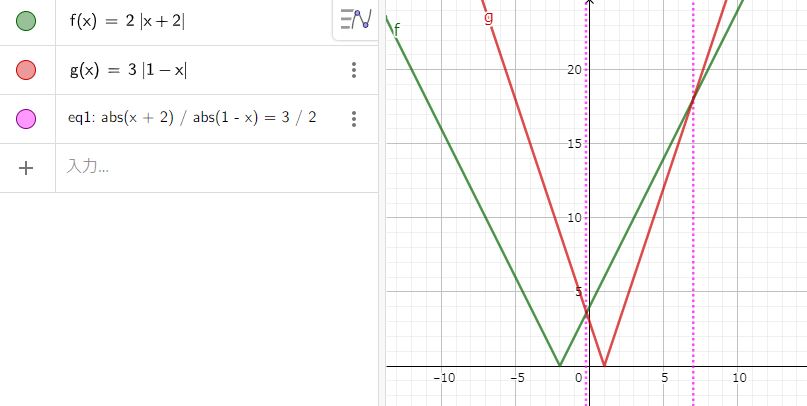
$ 2 \left| x + 2 \right| = 3 \left| 1-x \right| $
この数式を fx-JP900 にキー入力して、ソルブ計算をすると、面白い結果が出て来ます。
$ -2 \leqq x \leqq 1 $ の値を $ x $ にキー入力すると 内分点の値が出てくる
$ \cancel{ x \leqq -2,~~1 \leqq x } ~ \textcolor{red}{ x \lt -2,~~1 \lt x } $ (2022-08-10 修正) の値を $ x $ にキー入力すると 外分点の値がでてくる
この理由は、下記のグラフの交点からピンと来るのではないでしょうか?
おっと!
すみません、もうこんな時間になってしまいました。
もう少し詳細をお話したいのですが、今日はこのへんで。
すみません。m( _ _;)m
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
8月5日に内分点の問題を例に「$ y=x $ の $ y $」と「$ f(x)=x $ の $ f(x) $」との違いについて書いてみました。
今日はこの問題を利用して、数直線上の値と、絶対値記号の関係について考えて行こうと思います。

まずは8月5日に取り上げた問題を書いておきます。
数直線上に、点 $ A $ と点 $ B $ があります。点 $ A $ は $ -2 $ の所。点 $ B $ は $ 1 $ のところです。
$ AB $ を $ 3:2 $ に内分する点 $ P $ は、数直線上のどの位置にくるでしょう?
$ AB $ を $ 3:2 $ に内分する点 $ P $ は、数直線上のどの位置にくるでしょう?
一般に数直線上の2点 $ A,~B $ に対して $ m : n $ に内分する点外分する点の位置 $ x $ を計算するには、公式がありますよね。
下記に示してみますと…
内分点は $ x = \displaystyle \frac{ na + mb }{ m + n } $
外分点は $ x = \displaystyle \frac{ -na + mb }{ m - n } $
となります。(右画像参照)
さて、この公式を覚えることは簡単です。
それに内分点を求めるには $ AP : PB = (x-a) : (b-x) = m : n $ の式から、その公式を導くことも出来ますよね。大したことではないでしょう。
でもこの公式、内分点と外分点の関係がどうして $ n $ の $ \cancel{ \mp } $ プラス・マイナス (2022-08-10 修正) に関係してくるのか、ちゃんと説明しようとすると言葉を失ったりしますよね。
なかなか難しいです。
そもそも内分点と言うのは分かりますが、外分点と言うのはどんな理由から存在している点なんでしょうかね?内分点と外分点、それと $ n $ と $ -n $ の関係とはどんなものなんでしょうか?
これは、結論から言いますと絶対値記号を使うと場合分けが必要になることに関係があります。
絶対値記号を外す時には、内部がマイナス値かプラス値かで場合分けをする必要がありますよね。内部がマイナス値だった場合は、全体をマイナス記号で括らなくてはなりません。
例) $ \left| x + 2 \right| $
・$ -2 \leqq x $ の場合
$ (x + 2) $
・$ x \lt -2 $ の場合
$ -(x + 2) $
でも、この場合分けと内分点・外分点は残念ながら「
絶対値記号を外す時の場合分けと、内分点・外分点の違いを表す $ n,~-n $ がどう対応しているのか?
それが分かると、公式も気持ちよく利用できるようになるんですけどね。私は高校時代から今まで、気持ちよく利用できていなかったんです。( ^^;
でもやっと、理解
そのきっかけは、先に示した問題の内分点を、fx-JP900 のソルブ機能を使って答えを計算したことにあります。
$ AB $ を $ 3:2 $ に内分する点 $ P $ の数直線上の値を $ x $ とすると下記の数式が成立するはずです。
$ AP:PB = 3:2 $ より
$ 2 \left| x + 2 \right| = 3 \left| 1-x \right| $
この数式を fx-JP900 にキー入力して、ソルブ計算をすると、面白い結果が出て来ます。
$ -2 \leqq x \leqq 1 $ の値を $ x $ にキー入力すると 内分点の値が出てくる
$ \cancel{ x \leqq -2,~~1 \leqq x } ~ \textcolor{red}{ x \lt -2,~~1 \lt x } $ (2022-08-10 修正) の値を $ x $ にキー入力すると 外分点の値がでてくる
この理由は、下記のグラフの交点からピンと来るのではないでしょうか?

おっと!
すみません、もうこんな時間になってしまいました。
もう少し詳細をお話したいのですが、今日はこのへんで。
すみません。m( _ _;)m
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(7361)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



