時空 解 さんの日記
2022
9月
24
(土)
09:42
本文
皆さんこんにちは、時空 解です。
今日は21日に放送された「笑わない数学」の第11回目放送、確率論を観た感想を書いてみたいと思います。
今回といちだんと面白かったです。NHK + でまだ視聴できますので、下にリンクを貼っておきます。
・笑わない数学 確率論 配信期限 :9/28(水) 午後11:29 まで
今回の放送の内容は、大きく3つに分けられると思います。今日はその一つをご紹介しましょう。
視聴者の掴みの問題ですね。とても興味深い問題を紹介してくれました。
その問題は
「モンティ・ホール問題」
と言う名前で有名なものなんだそうです。YouTube で検索してみると、けっこうな数が出て来ます。
例えば下記
・【目からウロコ】”人類最高のIQ” vs ”全米の数学者”!「モンティ・ホール問題」
竹内 薫さんも下記のサイトを書いていますね。
・最後に選択を変えると得か? 損か? 「モンティ・ホール問題」
問題の内容はこうです。
さて、この問題は、扉を変更した方が得か、損か、それとも変わらないか? と言う問題です。
うーむ…直感的には損も得もない気がしますよね。でもこれが違うんです!
番組内では、上記の動画やサイトとは違う解説の方法を取っています。


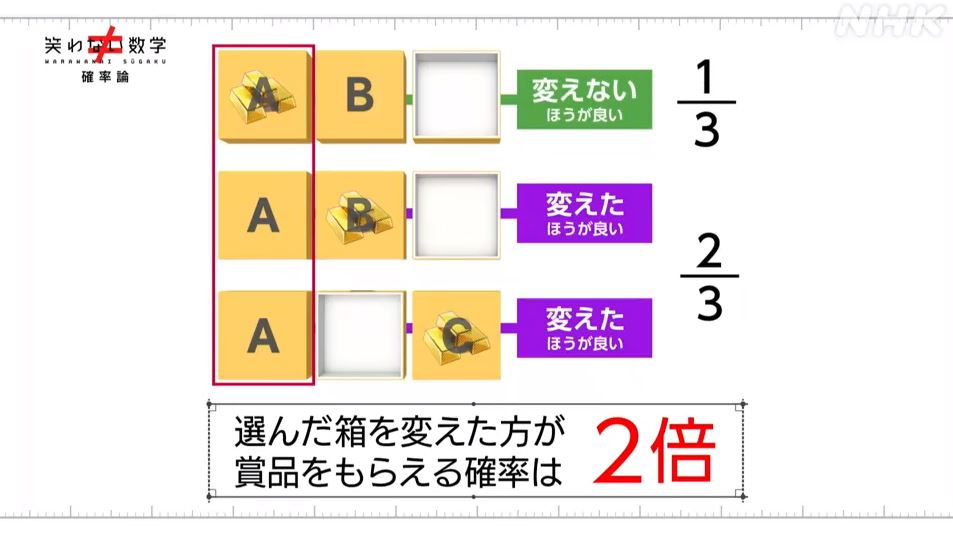
最初に3つから1つを選んでいるので、当たりの確率は $ \displaystyle \frac{ 1 }{ 3 } $
この状態から…この状態から、と言うのが重要ですよね。この状態から、残りの2つのうちはずれがどちらかを教えて貰えると言うことですからね。
最初に選んだ1つが当たりなのか外れなのかを、その場合分けが必要だと言うことです。
・自分が当たりを選んでいる場合
・自分がはずれを選んでいる場合
この場合分けをして、それぞれの確率を確認しないと正しい答えが出て来ないと言うことなんですね。
いやはや、やっぱり確率は奥が深いですね。
では、放送の内容の残り2つは、また明日、明後日にでも。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
今日は21日に放送された「笑わない数学」の第11回目放送、確率論を観た感想を書いてみたいと思います。
今回といちだんと面白かったです。NHK + でまだ視聴できますので、下にリンクを貼っておきます。
・笑わない数学 確率論 配信期限 :9/28(水) 午後11:29 まで
今回の放送の内容は、大きく3つに分けられると思います。今日はその一つをご紹介しましょう。
視聴者の掴みの問題ですね。とても興味深い問題を紹介してくれました。
その問題は
「モンティ・ホール問題」
と言う名前で有名なものなんだそうです。YouTube で検索してみると、けっこうな数が出て来ます。
例えば下記
・【目からウロコ】”人類最高のIQ” vs ”全米の数学者”!「モンティ・ホール問題」
竹内 薫さんも下記のサイトを書いていますね。
・最後に選択を変えると得か? 損か? 「モンティ・ホール問題」
問題の内容はこうです。
出題者曰く
「3つの扉 A, B, C (箱でもなんでも、とにかく3つの選択肢) のうち、1つの扉の向こう側には新車があります。もしその扉を当てることができたら、その新車を差し上げます」
と言う状況で、最初にあなたが扉 A を選んだとしましょう。
そしたら出題者が、残りの2つの扉 B, C のうちの1つを開けてみせてくれました。その扉 (例えば B ) ははずれの扉でした。
さて、この時に出題者から
「今選んでいる扉 A のままで良いですか?」
と問われたら、あなたならどうしますか?
今のままの 扉 A で行きますか?
それとも開かれていない扉 (例えば C ) に換えますか?
「3つの扉 A, B, C (箱でもなんでも、とにかく3つの選択肢) のうち、1つの扉の向こう側には新車があります。もしその扉を当てることができたら、その新車を差し上げます」
と言う状況で、最初にあなたが扉 A を選んだとしましょう。
そしたら出題者が、残りの2つの扉 B, C のうちの1つを開けてみせてくれました。その扉 (例えば B ) ははずれの扉でした。
さて、この時に出題者から
「今選んでいる扉 A のままで良いですか?」
と問われたら、あなたならどうしますか?
今のままの 扉 A で行きますか?
それとも開かれていない扉 (例えば C ) に換えますか?
さて、この問題は、扉を変更した方が得か、損か、それとも変わらないか? と言う問題です。
うーむ…直感的には損も得もない気がしますよね。でもこれが違うんです!
番組内では、上記の動画やサイトとは違う解説の方法を取っています。



最初に3つから1つを選んでいるので、当たりの確率は $ \displaystyle \frac{ 1 }{ 3 } $
この状態から…この状態から、と言うのが重要ですよね。この状態から、残りの2つのうちはずれがどちらかを教えて貰えると言うことですからね。
最初に選んだ1つが当たりなのか外れなのかを、その場合分けが必要だと言うことです。
・自分が当たりを選んでいる場合
・自分がはずれを選んでいる場合
この場合分けをして、それぞれの確率を確認しないと正しい答えが出て来ないと言うことなんですね。
いやはや、やっぱり確率は奥が深いですね。
では、放送の内容の残り2つは、また明日、明後日にでも。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(9772)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



