時空 解 さんの日記
2022
10月
3
(月)
09:31
本文
皆さんこんにちは、時空 解です。
2日前にも書きましたが、
「青チャート式数学II」の "基本例題136" と "基本例題139"
この2つの答えの矛盾を正しく理解することが出来てません。
うーむ…
この二日間、こだわっているので次に進めない状況でした。
これは良くないです。
そう想って、今日の朝に矛盾は矛盾として履歴に残しておいて、次に進むことにしました。次に進んで行く中で、この2つの矛盾を解決するヒントが見つかるかも知れませんしね。
この2日間ずっと頭の中で引っかかっていますが、そうこうしているうちに数学の学習をしなくなってしまいそうです。
これではいけません、前に進まなくちゃね…こんな状況の中、昨日は録画してあった「笑わない数学」の最終回 "ガロア理論" を視聴しました。 おおーっ!
おおーっ!
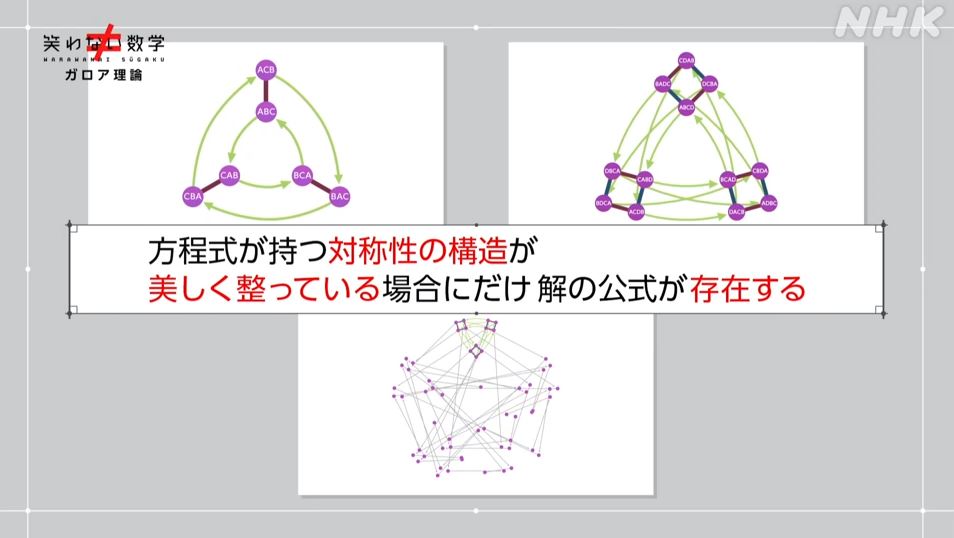
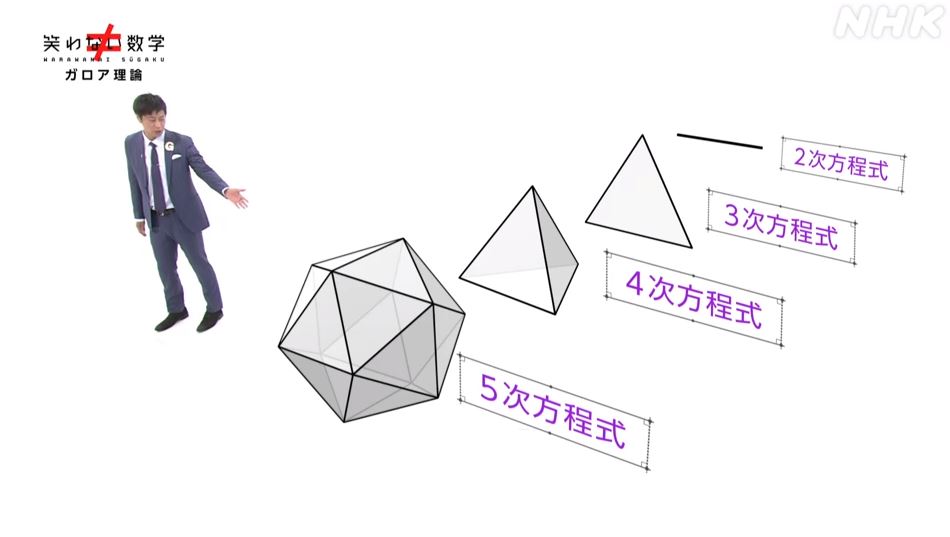

今まで何のことやら分からないまま、群だの環だの、一対一の集合など、ガロア理論の入り口で挫折していた私でしたが、この番組を視聴したおかげで理解するための糸口が見えた気がしました。
対称性の発見…と言うか着眼点が対称性と言うことかな?
ともかく一度視聴してみてください。
・「笑わない数学」 ガロア理論 配信期限 :10/5(水) 午後11:29 まで
どうして5次方程式には解の公式が存在しないのか?
その理由がこの対称性から分かるのだそうです。
青チャート式数学で方程式の問題を学習している時に、
「どうしてこんな当たり前のようなことを、こだわって書くのかなぁ?」
と思っていたものがあります。
それが
・対称式と交代式
です。
きっとこれが現代数学の夜明けともいえるほどの意味につなかっているのでしょうかね…そんな気がしました。
ともかく分からないことにこだわるのは止めて、キチンと「分からない点」を押さえておいて、前に進んで行こうと思った昨日です。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
2日前にも書きましたが、
「青チャート式数学II」の "基本例題136" と "基本例題139"
この2つの答えの矛盾を正しく理解することが出来てません。
うーむ…
この二日間、こだわっているので次に進めない状況でした。
これは良くないです。
そう想って、今日の朝に矛盾は矛盾として履歴に残しておいて、次に進むことにしました。次に進んで行く中で、この2つの矛盾を解決するヒントが見つかるかも知れませんしね。
この2日間ずっと頭の中で引っかかっていますが、そうこうしているうちに数学の学習をしなくなってしまいそうです。
これではいけません、前に進まなくちゃね…こんな状況の中、昨日は録画してあった「笑わない数学」の最終回 "ガロア理論" を視聴しました。



今まで何のことやら分からないまま、群だの環だの、一対一の集合など、ガロア理論の入り口で挫折していた私でしたが、この番組を視聴したおかげで理解するための糸口が見えた気がしました。
対称性の発見…と言うか着眼点が対称性と言うことかな?
ともかく一度視聴してみてください。
・「笑わない数学」 ガロア理論 配信期限 :10/5(水) 午後11:29 まで
どうして5次方程式には解の公式が存在しないのか?
その理由がこの対称性から分かるのだそうです。
青チャート式数学で方程式の問題を学習している時に、
「どうしてこんな当たり前のようなことを、こだわって書くのかなぁ?」
と思っていたものがあります。
それが
・対称式と交代式
です。
きっとこれが現代数学の夜明けともいえるほどの意味につなかっているのでしょうかね…そんな気がしました。
ともかく分からないことにこだわるのは止めて、キチンと「分からない点」を押さえておいて、前に進んで行こうと思った昨日です。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6275)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



