皆さんこんばんは、時空 解です。

さっきブログを投稿したばかりですが、新たに数学的に良い情報が手に入りましたので投稿します。

５次方程式がどうして解けないのか？
その証明を、ガロアがどんな形で行ったのかを知ることができます。

それが下記の動画です。
・3-2. 五次方程式が代数的に解けないわけ - 2015/5/22



動画の出だし１分と２１秒ほどは、解説者と会場の方とで和気あいあいとやっています。この部分でなんだかちゃんとした解説が期待できない気がして来ます。ですので動画のスタートポイントを１分２１秒からにしてあります。ご了承くださいませ。

さて、数日前に「笑わない数学」ガロア理論　を視聴して対称性がガロア理論のポイントであることが分かりました。
でも、その対称性って、対称式で言っている対称性と同じ「対称」なんですかね？

そんな疑問が頭の片隅に残っていました。それで…かなりガロア理論について気に成り出していました。

そんなこんなで、今日目眩がするので布団で横になっていたのですが…
YouTubeチャンネルでガロア理論、特に、５次方程式がどうして代数的に解けないのか？それを調べたくなったんですよね。( ^^;

ガロアがどう考えたのか？

うーむ…知りたい。

布団から起き出して、アマゾンで書籍を検索していたら、ヒントがありました。カスタマーレビューですね。
・概観するのに良いかも

上記のレビューの中に動画「五次方程式が代数的に解けないわけ」が紹介されていたんです。
視聴してみて驚きました！　　なるほど！

まず、この動画の優れている点は、２次方程式がどうして代数的に解けるのか？
それを解説し、ガロア理論に結びつけて行く点です。

「代数的に解ける」と言うことを２次方程式の「解と係数の関係」より示し、これを足場にして３次方程式、４次方程式、そして五次方程式へと解説を進めるのです。

どうして「巡回群」じゃないと代数的に解けないのか？　と言う解説まではされていませんが、ガロアがどう考えを進めて「証明」に至ったのかは、良く分かりました。
  
 

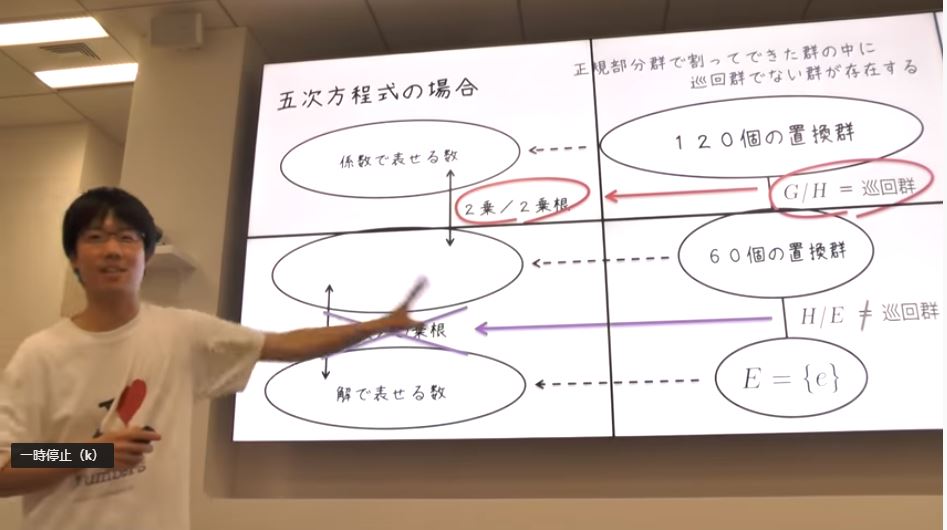
上記がガロアのアイディアなんですね。
とても勉強になりました。

うーむ、なんだか体調も良くなってきましたよ。
では、今日はこのへんで…プレバトでも観てのんびりします。