時空 解 さんの日記
2022
10月
12
(水)
09:51
本文
皆さんこんにちは、時空 解です。
昨日の夜は、
「こんなムズい問題が1次の問題として出題されるのか?」
と、思わず声が出た問題を目の当たりにしました。
うーむ…これは難しい。解法がわからない。
第394回 2級1次 問題6

でも、この問題は表題にも書きました
「メネラウスの定理」
と言うものを知っていればすぐに解ける問題だったんですね。
今日の朝、やっと思い出しました。_| ̄|○
私はさんざん学習していたんです。ブログを検索してみたら出て来ました。( ^^;
例えば2021年01月20日の記事
・チェバの定理、メネラウスの定理を学習して想うこと2つ
1年と10ヶ月ほど前のことなのに…昨晩は全く思い出せなかった。ショックです。
いまいちど復習が必要ですね。「メネラウスの定理」を下に示しておきましょう。
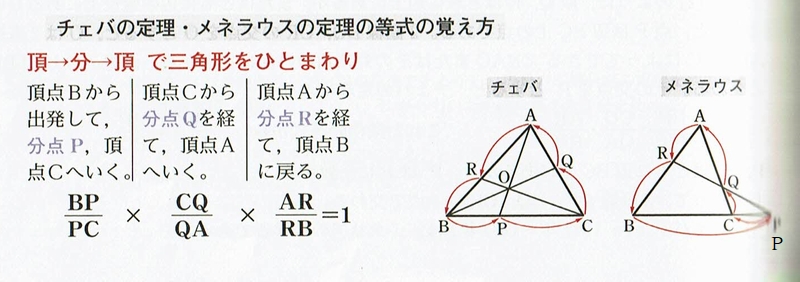
上記は「青チャート式数学A」に記載されている覚え方なのですが、第394回 2級1次 問題6の問題と比較してみると…
使われている記号 $ A,~B,~C,~R,~P,~Q $ と位置が全く同じです。
数学検定の出題の仕方が (1次検定だからかも知れませんが ) 親切ですね、なんだかホッとします。
公式がそのまま利用できます。
$ \displaystyle \frac{ BP }{ PC } \cdot \frac{ CQ }{ QA } \cdot \frac{ AR }{ RB } = 1 $ より
$ \displaystyle \frac{ 5 }{ 2 } \cdot \frac{ CQ }{ QA } \cdot \frac{ 2 }{ 4 } = 1 $
上式を整理すると
$ \displaystyle \frac{ CQ }{ QA } = \frac{ 4 }{ 5 } $
$ \therefore~~CQ : QA = 4 : 5 $
ところで、やっぱり丸暗記しても直ぐに忘れてしまいます。この定理の成り立ちを理解して、その成り立ちのすばらしさ (?) を味わえないとね。
中学・高校の頃だったら定理の成り立ち。考え方に
「おおっ! なるほど、メネラウスくんは頭が良いじゃないか」
なんて、上から目線で感動していたかも知れません。
若い頃はそんな私でした。ヤな奴ですが、そんな自分も懐かしいし、今では羨ましくもあります…。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
昨日の夜は、
「こんなムズい問題が1次の問題として出題されるのか?」
と、思わず声が出た問題を目の当たりにしました。
うーむ…これは難しい。解法がわからない。
第394回 2級1次 問題6

でも、この問題は表題にも書きました
「メネラウスの定理」
と言うものを知っていればすぐに解ける問題だったんですね。
今日の朝、やっと思い出しました。_| ̄|○
私はさんざん学習していたんです。ブログを検索してみたら出て来ました。( ^^;
例えば2021年01月20日の記事
・チェバの定理、メネラウスの定理を学習して想うこと2つ
1年と10ヶ月ほど前のことなのに…昨晩は全く思い出せなかった。ショックです。
いまいちど復習が必要ですね。「メネラウスの定理」を下に示しておきましょう。

上記は「青チャート式数学A」に記載されている覚え方なのですが、第394回 2級1次 問題6の問題と比較してみると…
使われている記号 $ A,~B,~C,~R,~P,~Q $ と位置が全く同じです。
数学検定の出題の仕方が (1次検定だからかも知れませんが ) 親切ですね、なんだかホッとします。
公式がそのまま利用できます。
$ \displaystyle \frac{ BP }{ PC } \cdot \frac{ CQ }{ QA } \cdot \frac{ AR }{ RB } = 1 $ より
$ \displaystyle \frac{ 5 }{ 2 } \cdot \frac{ CQ }{ QA } \cdot \frac{ 2 }{ 4 } = 1 $
上式を整理すると
$ \displaystyle \frac{ CQ }{ QA } = \frac{ 4 }{ 5 } $
$ \therefore~~CQ : QA = 4 : 5 $
ところで、やっぱり丸暗記しても直ぐに忘れてしまいます。この定理の成り立ちを理解して、その成り立ちのすばらしさ (?) を味わえないとね。
中学・高校の頃だったら定理の成り立ち。考え方に
「おおっ! なるほど、メネラウスくんは頭が良いじゃないか」
なんて、上から目線で感動していたかも知れません。
若い頃はそんな私でした。ヤな奴ですが、そんな自分も懐かしいし、今では羨ましくもあります…。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(7853)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



