皆さんこんにちは、時空 解です。

数学検定の２級２次でも定番としてよく出題されるのが、最後の問題７に出てくる微積分の問題。
でも、その次に良くでてくるのが２次方程式のグラフに関する問題ですよね。
２次方程式のグラフの問題と言ってもいろいろなパターンがありますけどね。( ごめんなさい m( _ _;)m  )

とにかく、青チャート式数学で言えば、Iの第３章：２次関数　の章の内容です。

例えばこんな問題。
第390回　2022年６月４日 実施の２級２次、問題１. (選択)


受検を受けた当日、この問題を目の当たりにしてちょっと頭の中が真っ白くなりそうだったことを想い出します。
なんと言っても、こんな形式の出題はなかなかお目に掛かりませんからね。( ^^;

でも、この問題もグラフをキッチリとイメージ出来ると
「なんだ、けっこう簡単な問題だなぁ」
なんて想えるのではないでしょうか？　

とにく答えを知ってからの復習だとね。

ポイントとしては $ x = 1 $ のところに交点があることでしょう。

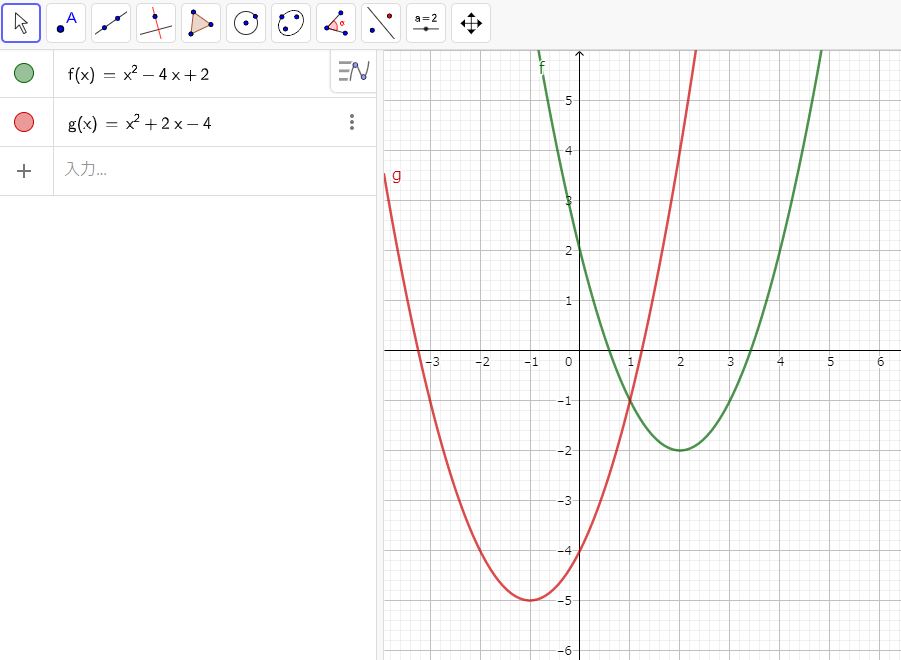
グラフを Geogebra で描いてみました。
右にそれを示します。このグラフを描くと、設問の (2) の答えが明快に見えてきますよね。

「この問題は解法の過程を記述せずに答えだけを書いてください。」
と注意書きがされるのも当然でしょう。

ただし丁寧に解答して行かないと、ケアレスミスをします。
試験時間が限られていますしね。焦ると勘違いします、気を付けましょう

・・・この問題、検定では焦ってしまい 0.4 点しか取れなかった私です…。＿|￣|○

では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )