皆さんこんにちは、時空 解です。

中学レベルの数学は、問題を解くポイントが一つで、それに気が付けば解ける。
そんな問題が殆どですよね…。

例えばどんな公式を利用すれば解けるのか、と言った具合です。

でも高校の数学は違います。利用する公式は当たり前に分かっても、変数の範囲があったり、場合分けをする必要が多々あったり…その判断が複雑です。

１０月２６日２６日にご紹介した
・「新課程 青チャート式数学II」重要例題１４９ (または １４４)

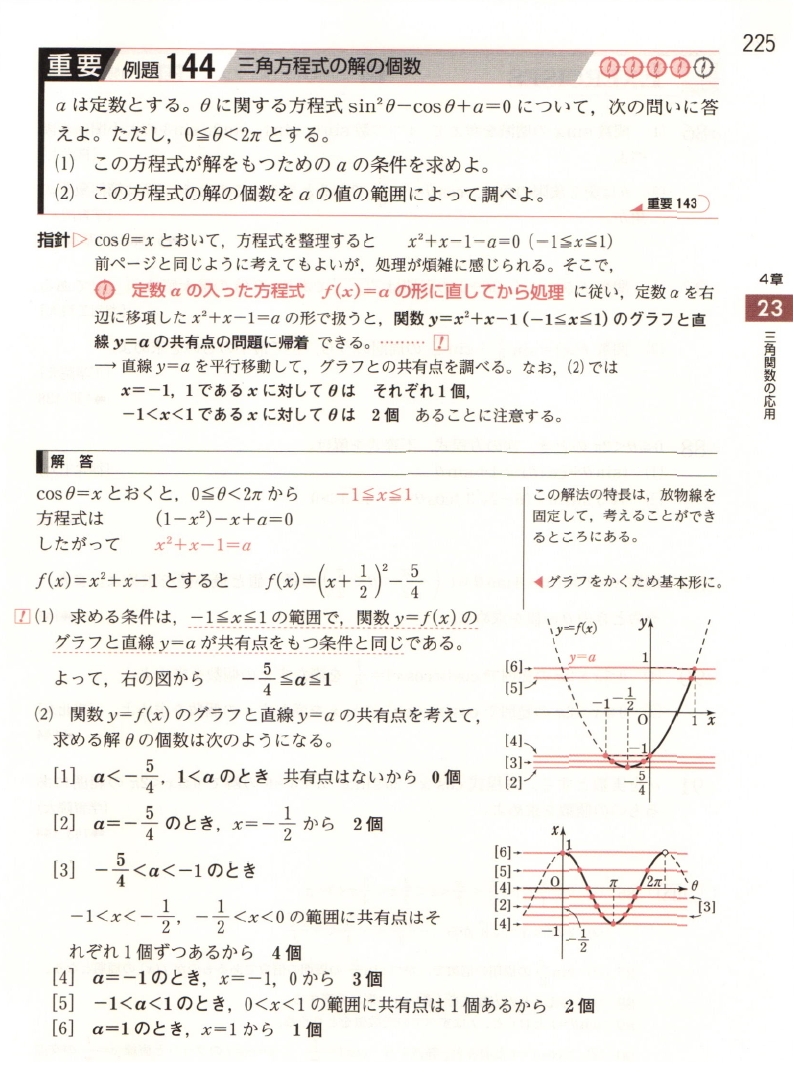
この問題、設問の (1) については、なんとか $ f(x) = a $ の形にせずに解くことが出来ました。
技をつかわずに、まずは王道のやりかたで解けましたので、納得できたのですが…。

設問の (2) は取っつき難いです。( ^^;
これも $ f(x) = a $ に変形せずに、王道のやり方で解けるのでしょうかね？…いったいどうやればいいのでしょう？
分からなかったので今日は止めにしましたが…

高校生だったころの自分なら、$ f(x) = a $ の形で解く解法のみで次に進んでいたでしょう。

でも今はなんだかこだわってしまいます。
「 $ a $ と $ x^2 + x -1 $ との交点による解法のみで済ませていいのかぃ！」
なーんて、ちょっとチャート式数学に突っ込みを入れている私です。

これがいい事なのか悪い事なのか…とにかく解いた気がしない今日でした。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )