時空 解 さんの日記
2022
10月
30
(日)
23:21
本文
皆さんこんにちは、時空 解です。(すみません、下書き書いただけで、それを投稿するの忘れてました m( _ _;)m )
今日の朝、再び「青チャート式数学II」の重要例題149 (144) を考えてみたら…
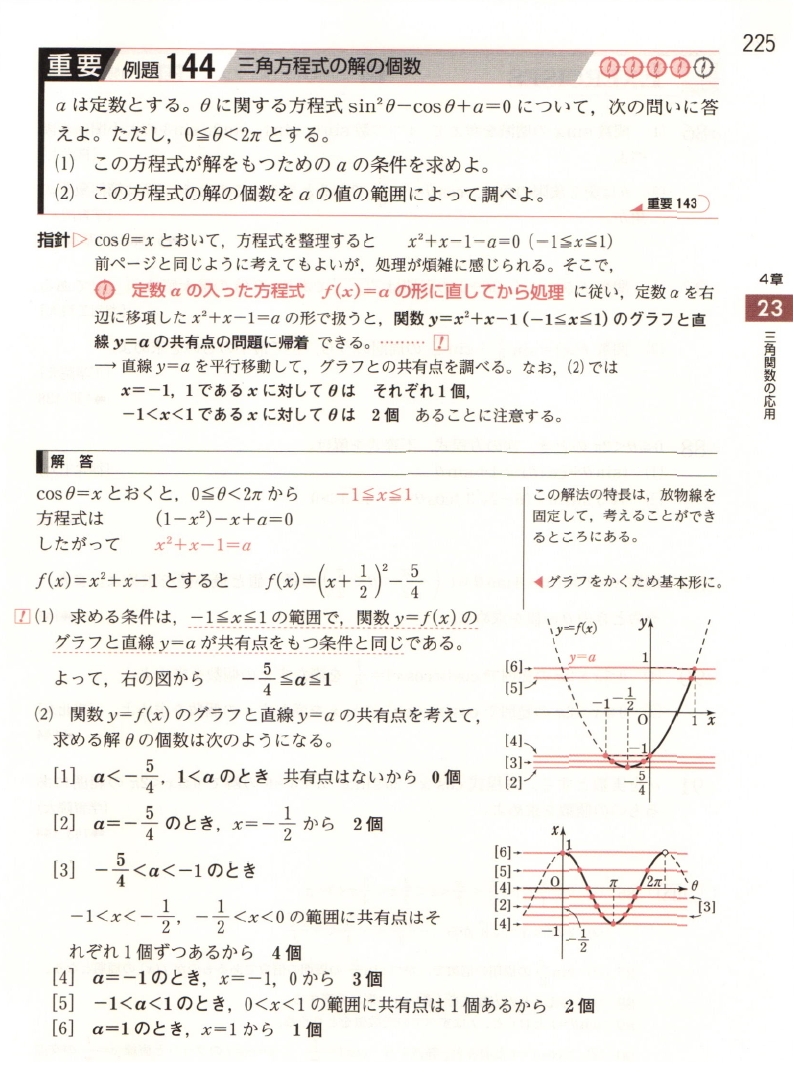
解答のように $ f(x) = a $ に帰着する方法と、そうでない方法、$ f(x) -a = 0 $ を比較して、圧倒的に $ f(x) = a $ の方が考え易いことが分かりました。
それに昨日は
「 $ f(x) = a $ なんて技を使わないで王道で考えたらどうなるだろう…分からない」
と、自分は分からない状態だったはずなんですが…。
あっ! なんだ $ f(x) = a $ を使わない方法は $ f(x) -a = 0 $ でいいんだ、と今日の朝に気が付きました。
なんだ $ f(x) = a $ を使わない方法は $ f(x) -a = 0 $ でいいんだ、と今日の朝に気が付きました。
$ f(x) -a = 0 $ だと確かに $ t^2 + t -1 -a $ の双曲線グラフ自体を $ a $ 値の変化に合わせて上下にスライドさせて考えなくてはなりません。
これは面倒です。( ^^;
やっぱり $ t^2 + t -1 $ に対して、横軸 $ a $ を考え、双曲線グラフとの交点を考える方が楽です。
これこそを王道と言っても過言ではないくらいですよね。
設問 (1) は、理解を深めるために王道 (場合分けをして、その一つ一つを計算する) で考えることも有意義でしたが、設問 (2) は王道で考えることに有意義な点はなさそうです。
昨日は
「設問 (2) も王道で考えるとめんどうくさそうだなぁ…」
なんて感じた瞬間
「あーーーっ、難しそう!」
と、思考を停止した私でしたね。
$ f(x) -a = 0 $ の数式が頭に浮かばなかったのですよね… ( ^^;
この理由は、きっと数学の学習はもうしたく無くなっていたんでしょう。
そろそろ数学の学習時間が終わりそうでもありましたし、ちょっと変な方向に頭が回った瞬間に
「これは面倒だ」
と無意識に想ったのだと想います。
それを
「難しい」
と、意識たのでしょう。
こんなことを繰り返していると、時間がないとか、面倒くさいと想った時に
「難しい問題だ」
と、自分で自分を想い込ませる癖が付いてしまいそうですよね。
これこそを気を付けないとね。間違った学習をしていることになります。
もっとシンプルな解決法も探ってみる…これも数学の重要な要素のはずなのにね…気を付けたいと思います。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
今日の朝、再び「青チャート式数学II」の重要例題149 (144) を考えてみたら…

解答のように $ f(x) = a $ に帰着する方法と、そうでない方法、$ f(x) -a = 0 $ を比較して、圧倒的に $ f(x) = a $ の方が考え易いことが分かりました。
それに昨日は
「 $ f(x) = a $ なんて技を使わないで王道で考えたらどうなるだろう…分からない」
と、自分は分からない状態だったはずなんですが…。
あっ!
$ f(x) -a = 0 $ だと確かに $ t^2 + t -1 -a $ の双曲線グラフ自体を $ a $ 値の変化に合わせて上下にスライドさせて考えなくてはなりません。
これは面倒です。( ^^;
やっぱり $ t^2 + t -1 $ に対して、横軸 $ a $ を考え、双曲線グラフとの交点を考える方が楽です。
これこそを王道と言っても過言ではないくらいですよね。
設問 (1) は、理解を深めるために王道 (場合分けをして、その一つ一つを計算する) で考えることも有意義でしたが、設問 (2) は王道で考えることに有意義な点はなさそうです。
昨日は
「設問 (2) も王道で考えるとめんどうくさそうだなぁ…」
なんて感じた瞬間
「あーーーっ、難しそう!」
と、思考を停止した私でしたね。
$ f(x) -a = 0 $ の数式が頭に浮かばなかったのですよね… ( ^^;
この理由は、きっと数学の学習はもうしたく無くなっていたんでしょう。
そろそろ数学の学習時間が終わりそうでもありましたし、ちょっと変な方向に頭が回った瞬間に
「これは面倒だ」
と無意識に想ったのだと想います。
それを
「難しい」
と、意識たのでしょう。
こんなことを繰り返していると、時間がないとか、面倒くさいと想った時に
「難しい問題だ」
と、自分で自分を想い込ませる癖が付いてしまいそうですよね。
これこそを気を付けないとね。間違った学習をしていることになります。
もっとシンプルな解決法も探ってみる…これも数学の重要な要素のはずなのにね…気を付けたいと思います。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6469)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



