皆さんこんにちは、時空 解です。

昨日は天気も穏やかな良い日でしたね。
数学検定の提携会場受検に行ってきましたが、受検中も寒さを感じることなく問題を解くことが出来ました。
会場 (公文式の塾) も以前からのお馴染みの会場でしたしね。確か三度目ですかね。

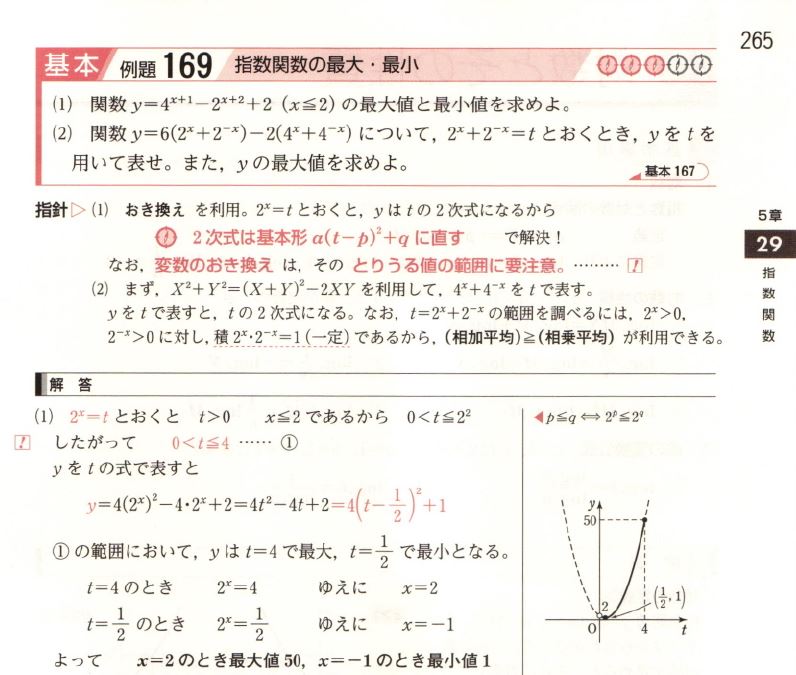
さて、そんな悪くない環境の中、２級２次の選択問題１を見てちょっとびっくりした次第です。

「これは… "青チャート式数学II" の基本例題１７５、設問 (1) をちゃんと理解出来ていれば解けたなぁ…」

という問題だったんです。(数研出版さんの解説動画にリンクを貼っておきました)

この問題のポイントは $ 2^x = t $ と変数を置き換えて解くところにあるのですが、昨日の２級２次の選択問題１も、まさに変数の置き換えを理解しているか否か？　…を問う問題でした。

問題の内容としては $ t = x^2 -2x -3 $ として、与式 $ f(x)=(x^2-2x -2)(x^2 -2x -4) $ の最大値と最小値、その時の $ x $ の値を求める問題です。
与えられている $ x $ の範囲は $ -3 \geqq x \geqq 3 $。

$ t $ の範囲を求めることがまずは一つ目のステップとなりますが、それが設問 (1) にも成っている問題でした。
(数式は思い出して書き出したものですので、間違っているかも知れません。ご了承ください)

うーむ…ちょうど「青チャート式数学II」の基本例題１７５ (改訂版では１６９) で変数の置き換えを学習しているところでしたが。
「チャート式数学の学習は数検が終わってからにしよう」
なんて想ってね。

置き換えの仕方… $ x $ と $ t $ との対応…どう頭の中で整理したらいいのか？
そこの理解を保留にしていたところだったんです。( ^^; 

…いつもの習慣として「青チャート式数学II」をきっちり学習していれば…＿|￣|○

$ f(x) = (t^2 + 1)(t^2 - 1) $

上記のように式変形をして $ t $ のグラフを描き $ x $ に対応した $ t $ の範囲を求めましたが…正しく解答できたかは自信ありません。
$ f(x) $ の最大値、最小値も求められなかったんです。

うーむ…この選択問題１で $ 1 $ 点が取れたのなら、２級２次に合格できたかもなぁ…

いやいや、他の答えられた問題も × かもしれませんしね…　

結局は今の私の実力がそのまま評価される、と言うことですね。
昨日も自分の数学力の足りなさを実感させられた次第です。
もっと勉強しないと…。

では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )