時空 解 さんの日記
2023
7月
15
(土)
09:40
本文
皆さん こんにちは、時空 解です。
応用問題に対する記述と言うのは、迷うものですよね。
…まぁ解答に自信のある時には
「えっ! そんな記述をするの?」
なんて、模範解答に対していちゃもんを言いたくなるほどでもありますが…模範解答をよく読み直してみると、自分の考えが浅いことに気が付くことはよくあることです。
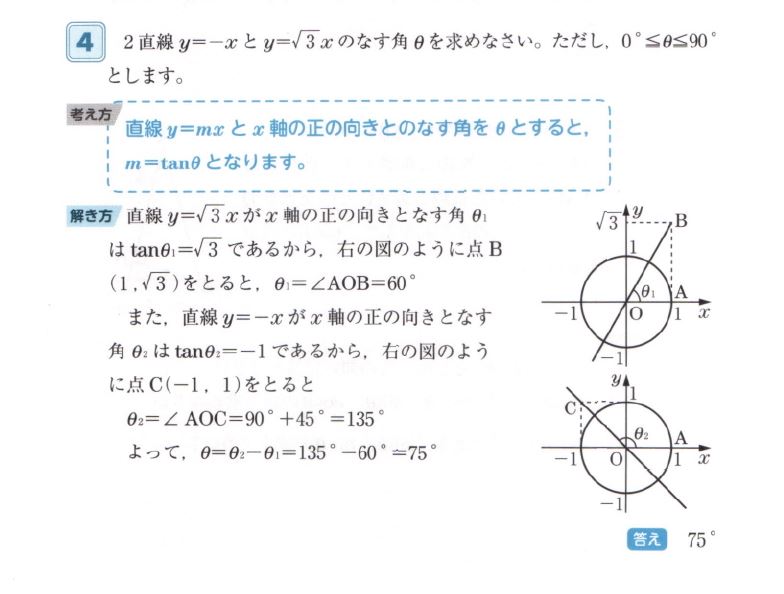
でもね…例えば右に示しておいた
・「2023年版 実用数学技能検定 要点整理 数学検定2級」67ページ、応用問題4
要点整理に載っている右の記述はどう思われますか?
うーむ…個人的にはなんだか良くない気がします。わかりにくい…
私なら下記のように記述したいと思っています。
この記述解答でも、私は減点されないと思いますが…どうでしょうかね?
やっぱり数学検定で上記の問題が出たら、模範解答を真似て答えを書いたほうがいいでしょうかね… ( ^^;
私は自分なりの記述を書いて、結果を待つ方を選ぼうかなー…なんて思います。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
応用問題に対する記述と言うのは、迷うものですよね。
…まぁ解答に自信のある時には
「えっ! そんな記述をするの?」
なんて、模範解答に対していちゃもんを言いたくなるほどでもありますが…模範解答をよく読み直してみると、自分の考えが浅いことに気が付くことはよくあることです。

でもね…例えば右に示しておいた
・「2023年版 実用数学技能検定 要点整理 数学検定2級」67ページ、応用問題4
要点整理に載っている右の記述はどう思われますか?
うーむ…個人的にはなんだか良くない気がします。わかりにくい…
私なら下記のように記述したいと思っています。
2直線のそれぞれの、$ x $ 軸の正の向きとのなす角度は $ \tan \theta $ で表されるから
$ y = -x $ のグラフは $ x $ 軸に対して $ \tan \theta_1 = -1 $。これより $ \theta_1 = -45^\circ $
$ y = \sqrt{ 3 } x $ のグラフは $ x $ 軸に対して $ \tan \theta_2 = \sqrt{ 3 } $。これより $ \theta_2 = 60^\circ $
したがって与えられた2直線のなす角 $ \theta $ は $ \theta_1 $ と $ \theta_2 $ より $ 105^\circ $ または $ 75^\circ $。
$ 0^\circ \leqq \theta \leqq 90^\circ $ より
$ \underline { Ans: \textcolor{green}{ 75^\circ } } $
$ y = -x $ のグラフは $ x $ 軸に対して $ \tan \theta_1 = -1 $。これより $ \theta_1 = -45^\circ $
$ y = \sqrt{ 3 } x $ のグラフは $ x $ 軸に対して $ \tan \theta_2 = \sqrt{ 3 } $。これより $ \theta_2 = 60^\circ $
したがって与えられた2直線のなす角 $ \theta $ は $ \theta_1 $ と $ \theta_2 $ より $ 105^\circ $ または $ 75^\circ $。
$ 0^\circ \leqq \theta \leqq 90^\circ $ より
$ \underline { Ans: \textcolor{green}{ 75^\circ } } $
この記述解答でも、私は減点されないと思いますが…どうでしょうかね?
やっぱり数学検定で上記の問題が出たら、模範解答を真似て答えを書いたほうがいいでしょうかね… ( ^^;
私は自分なりの記述を書いて、結果を待つ方を選ぼうかなー…なんて思います。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(7824)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



