時空 解 さんの日記
2023
7月
17
(月)
09:17
本文
皆さん こんにちは、時空 解です。
表題にも書いた通り
「2023年版 実用数学技能検定 要点整理 数学検定2級」
の 72ページに載っている
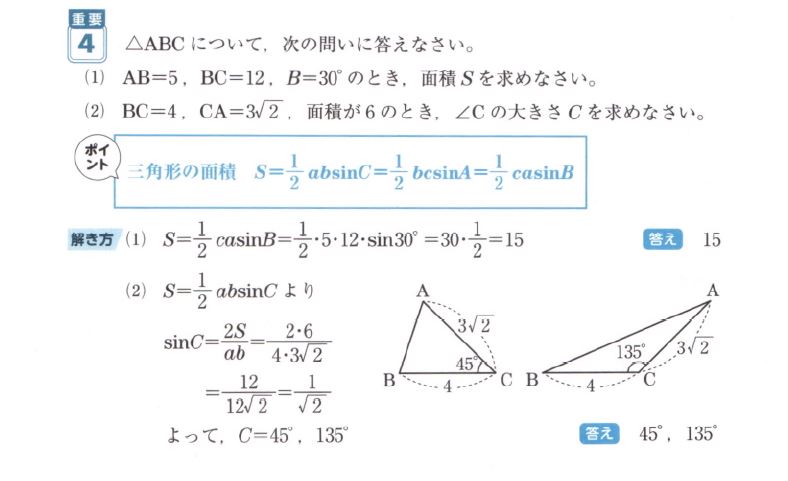
・練習問題 重要4
この問題は何が重要なのか? …と言えば、問いてみて答え合わせをしたときに
「あっ!」
と思った人は実感することと思います。
少なくとも私は実感しました。( ^^;
正弦定理と余弦定理のところで一緒に出てくる三角形の面積の公式は
$ S = \displaystyle { \frac{ 1 }{ 2 } ab \sin C = \frac{ 1 }{ 2 } bc \sin A = \frac{ 1 }{ 2 } ca \sin B } $
ですよね。この問題も公式に当てはめればすぐに解ける問題です。
でもね…。
設問の (2) は $ \sin C $ の角度を答えとして要求しています。
辺の長さを答えとして要求する問題については、答えがプラス値なんでね、あまり問題ではありませんが…
(しかし、例えば "辺 $ AB \gt 0 $ なので" という注意書きを記述しないと $ 0.2 $ 点くらいは減点されるかもね)
でも
$ \sin C = \displaystyle \frac{ 1 }{ \sqrt{ 2 } } $ の $ \angle C $ は注意が必要です。
答えが2つあるからね。きっと $ 0.4 $ 点ぐらい減点される気がします。
三角形の鋭角と鈍角…自分としても当たり前にわかっているつもりでしたが…いざ出題されると見落とします…。_| ̄|○
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
表題にも書いた通り
「2023年版 実用数学技能検定 要点整理 数学検定2級」
の 72ページに載っている

・練習問題 重要4
この問題は何が重要なのか? …と言えば、問いてみて答え合わせをしたときに
「あっ!」
と思った人は実感することと思います。
少なくとも私は実感しました。( ^^;
正弦定理と余弦定理のところで一緒に出てくる三角形の面積の公式は
$ S = \displaystyle { \frac{ 1 }{ 2 } ab \sin C = \frac{ 1 }{ 2 } bc \sin A = \frac{ 1 }{ 2 } ca \sin B } $
ですよね。この問題も公式に当てはめればすぐに解ける問題です。
でもね…。
設問の (2) は $ \sin C $ の角度を答えとして要求しています。
辺の長さを答えとして要求する問題については、答えがプラス値なんでね、あまり問題ではありませんが…
(しかし、例えば "辺 $ AB \gt 0 $ なので" という注意書きを記述しないと $ 0.2 $ 点くらいは減点されるかもね)
でも
$ \sin C = \displaystyle \frac{ 1 }{ \sqrt{ 2 } } $ の $ \angle C $ は注意が必要です。
答えが2つあるからね。きっと $ 0.4 $ 点ぐらい減点される気がします。
三角形の鋭角と鈍角…自分としても当たり前にわかっているつもりでしたが…いざ出題されると見落とします…。_| ̄|○
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(7529)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



