時空 解 さんの日記
2023
7月
22
(土)
09:44
本文
皆さん こんにちは、時空 解です。
積分の基本問題として、不定積分と定積分を求める問題がありますよね。

例えば下記の問題 (右画像参照)
この問題の与式をグラフで表すと下記のようになります。
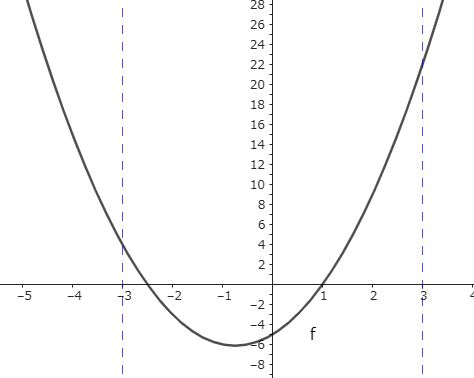
実は積分に関して今までずっと疑問に思っていたことがあったんです。
その疑問が上記の問題の与式をブラフ化することで解消されました。
定積分の値って…マイナス値が出てきてもいいんですね。( ^^;
なんとなくですが…今日の朝思ったことは
"定積分の値はプラス値でなくてはならない"
と言う想いです。
でもこれって、面積を求める場合ですよね。
ちなみに、上記の問題の設問 (2) で、定積分の値を求めるのではなく「面積」を求めるとなると下記の式
$ \displaystyle \int_{-3}^{ 3 } \left| 2x^2 + 3x -5 \right| dx $
これを計算することになります。
こうなると面倒です。
fx-JP900 を使えば $ f_{(x)} = 2x^2 + 3x -5 $ を絶対値記号で囲ってやって定積分計算操作すれば、答えをだせますが…
数学検定で答えを記述するとなると、場合分けが必要になりますからね。
$ \displaystyle \int_{-3}^{ 3 } \left| 2x^2 + 3x -5 \right| dx = \displaystyle \int_{-3}^{ -2.5 } (2x^2 + 3x -5) dx - \int_{-2.5}^{ 1 } (2x^2 + 3x -5) dx + \int_{1}^{ 3 } (2x^2 + 3x -5) dx $
考えてみれば $ x $ 軸よりも下の部分はマイナス値になるのだからね。これをプラス値として計算しないと面積は出てきません。
でも定積分の値としてならそのままのマイナス値でいいんですよね…これがいつの間にか
「プラス値でないとおかしい」
なんて印象になっていました。
基本問題もテスト前は一度、解いてみる必要がありますね。こんな勘違いをしていたなんて思いもよりませんでした。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
積分の基本問題として、不定積分と定積分を求める問題がありますよね。

例えば下記の問題 (右画像参照)
2023年_実用数学技能検定 要点整理 数学検定2級 より P160 基本問題 1 (重要)
関数 $ f_{(x)} = 2x^2 + 3x -5 $ について、次の問いに答えなさい。
(1) 不定積分 $ \displaystyle \int f(x) dx $ を求めなさい。
(2) 定積分 $ \displaystyle \int_{-3}^{ 3 } f(x) dx $ を求めなさい。
関数 $ f_{(x)} = 2x^2 + 3x -5 $ について、次の問いに答えなさい。
(1) 不定積分 $ \displaystyle \int f(x) dx $ を求めなさい。
(2) 定積分 $ \displaystyle \int_{-3}^{ 3 } f(x) dx $ を求めなさい。
この問題の与式をグラフで表すと下記のようになります。

実は積分に関して今までずっと疑問に思っていたことがあったんです。
その疑問が上記の問題の与式をブラフ化することで解消されました。
定積分の値って…マイナス値が出てきてもいいんですね。( ^^;
なんとなくですが…今日の朝思ったことは
"定積分の値はプラス値でなくてはならない"
と言う想いです。
でもこれって、面積を求める場合ですよね。
ちなみに、上記の問題の設問 (2) で、定積分の値を求めるのではなく「面積」を求めるとなると下記の式
$ \displaystyle \int_{-3}^{ 3 } \left| 2x^2 + 3x -5 \right| dx $
これを計算することになります。
こうなると面倒です。
fx-JP900 を使えば $ f_{(x)} = 2x^2 + 3x -5 $ を絶対値記号で囲ってやって定積分計算操作すれば、答えをだせますが…
数学検定で答えを記述するとなると、場合分けが必要になりますからね。
$ \displaystyle \int_{-3}^{ 3 } \left| 2x^2 + 3x -5 \right| dx = \displaystyle \int_{-3}^{ -2.5 } (2x^2 + 3x -5) dx - \int_{-2.5}^{ 1 } (2x^2 + 3x -5) dx + \int_{1}^{ 3 } (2x^2 + 3x -5) dx $
考えてみれば $ x $ 軸よりも下の部分はマイナス値になるのだからね。これをプラス値として計算しないと面積は出てきません。
でも定積分の値としてならそのままのマイナス値でいいんですよね…これがいつの間にか
「プラス値でないとおかしい」
なんて印象になっていました。
基本問題もテスト前は一度、解いてみる必要がありますね。こんな勘違いをしていたなんて思いもよりませんでした。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(7750)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



