皆さん こんにちは、時空 解です。

今日は新たな気分で「新課程 青チャート数学II」重要例題２２４ (改訂版では ２１４) を解いていました。
この問題、ややこしいのが場合分けです。
４つに場合分けをして考えて行かないと答えを出せません。

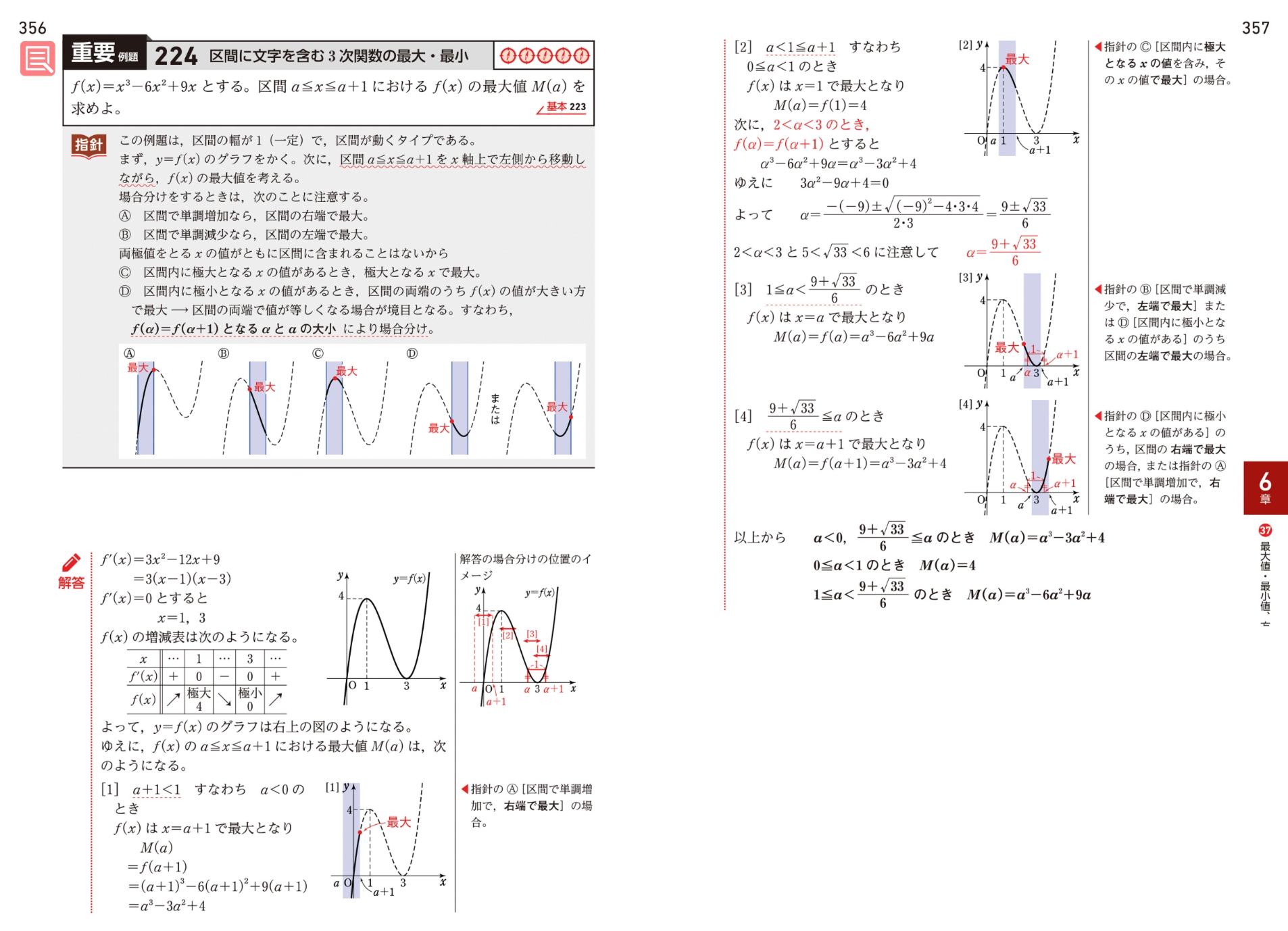
うーむ… (詳細は右画像参照のこと)

４つの場合分けの中で、特に難しいのが３つ目の場合分けの範囲です。
この範囲の求め方が私にはわかりませんでした。

青チャートの解答を見ても…ややこしくて理解できない。＿|￣|○
場合分けの [1]、[2] については順調に解いて行けたんですけどね。

$ f(x) $ の最大値が $ x = 3 $ の前後で同じになるところがあるのは分かるんですが…

でもね、その $ x = 3 $ の前後がどこなのか？　$ x $ の値の求め方が思い付きませんでした。

これをどうやって求めたら良いのか、その求め方がこの問題の最大のポイントでしょう。
私は解説動画を視聴するまで、青チャートの解答の下記の記述の意味が理解できませんでした。
 
解答で上記の記述を見ても、これでどうして $ x = 3 $ の前後の値が求められるのかがピンと来なかったんです。特に赤文字の部分ですね。

でも、やっぱり解説動画を視聴すると分かるもんですね。
逆に青チャートの解答 (文章、数式) だけだとね…どうしても頭に入ってこない。

と言うか入れる気に成れない？　( ^^;
と言うのが本音かな？　…ここが私の集中力、やる気の上限のように思えます。

もっと集中力や、やる気の上限を上げないといけないかも知れません。まぁとりあえずは、今日は解説動画が有ってよかったなぁと思った次第でした。


では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )