時空 解 さんの日記
2023
10月
9
(月)
09:31
本文
皆さん こんにちは、時空 解です。
数学の学習をしていて、三角関数の数式を変形しているときに、表題にも書いた数式がでてきたんですよね。
$ \sin α \cos α + \cos α \sin α $
「あ、これは…うーんと・・・ なんだっけ?」
お馴染みの三角関数の数式だとは分かったのですが…
ですけどね、角度 $ \theta $ が、$ α $ と $ β $ の二つの変数として表記されているのではなく、$ α $ 一つの数式でしたから。
それで混乱したのだと思います。
「左辺側はどうなるんだっけ…」
…いやいや、こんなことで混乱するようでは、
「もうろくしたと思われてしまう!」
なーんて…そんな心の葛藤を抱えながら数秒後にはなんとか左辺側を思い出しました。
そうそう、加法定理。$ \sin(α \pm β) = \sin α \cos β \pm \cos α \sin β $
これです。
さて、とにもかくにも、問題を解いている途中で $ \sin α \cos α + \cos α \sin α $ が出てきたんです。
ですから2倍角の公式として $ \sin 2 α $ と、つい変形してしまったんです。
なんと!
これが問題を解く途中での罠だったのかと思うと自分の数学力の無さにがっかりします…_| ̄|○
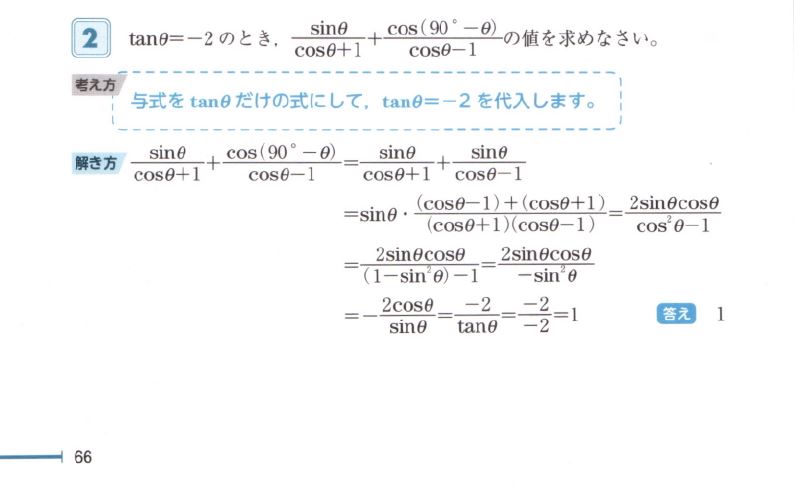
問題の解答を見てみてください。
(出典:2023年版 実用数学技能検定 要点整理2級 p66 2 より 右画像)
うっかり "加法定理・2倍角の公式" に捕らわれると答えにたどり着けないようにできているなんて…。
いやいや、自分で勝手に足を突っ込んだだけですかね…バカでした。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
数学の学習をしていて、三角関数の数式を変形しているときに、表題にも書いた数式がでてきたんですよね。
$ \sin α \cos α + \cos α \sin α $
「あ、これは…うーんと・・・ なんだっけ?」
お馴染みの三角関数の数式だとは分かったのですが…
ですけどね、角度 $ \theta $ が、$ α $ と $ β $ の二つの変数として表記されているのではなく、$ α $ 一つの数式でしたから。
それで混乱したのだと思います。
「左辺側はどうなるんだっけ…」
…いやいや、こんなことで混乱するようでは、
「もうろくしたと思われてしまう!」
なーんて…そんな心の葛藤を抱えながら数秒後にはなんとか左辺側を思い出しました。
そうそう、加法定理。$ \sin(α \pm β) = \sin α \cos β \pm \cos α \sin β $
これです。

さて、とにもかくにも、問題を解いている途中で $ \sin α \cos α + \cos α \sin α $ が出てきたんです。
ですから2倍角の公式として $ \sin 2 α $ と、つい変形してしまったんです。
なんと!
これが問題を解く途中での罠だったのかと思うと自分の数学力の無さにがっかりします…_| ̄|○
問題の解答を見てみてください。
(出典:2023年版 実用数学技能検定 要点整理2級 p66 2 より 右画像)
うっかり "加法定理・2倍角の公式" に捕らわれると答えにたどり着けないようにできているなんて…。
いやいや、自分で勝手に足を突っ込んだだけですかね…バカでした。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6326)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



