時空 解 さんの日記
2023
10月
18
(水)
15:25
本文
皆さん こんにちは、時空 解です。
今日も朝から理想の学習スタイル (下記) を試みて、今までの自分を乗り越えようとしていたのですが…
お昼を過ぎ、午後の2時にやっと、表題の問題が一つ理解がでたのみです。
復習に入る前にこんなに時間が掛かってしまうなんてね…朝から午後の2時までかかっていた問題と言うのは表題のとおり
「新課程 青チャート式数学II」基本例題223 (改訂版では 213)
です。

この問題は、実は3ヶ月前から理解するのに手こずっていた問題です。
(恥ずかしながら…)
・しばらく数学の問題を解いていないことを実感…「新課程 青チャート式数学II」基本例題223
振り返ってみると、今年の7月23日に実施された数学検定2級に不参加、欠席したことに始まりますね。
受検日当日、受験会場の駐車場に空きが無かったがため、受検を断念したのですけどね。
9月30日に実施された数学検定にはなんとか出席したのですが…。
とにかく今年の7月後半から今日にかけて、どうにも数学の学習が思うように進められなくなっているんです。
今日も朝から絶不調。( ^^;
でもなんとか、今は「新課程 青チャート式数学II」基本例題223」を理解することができて、こうしてブログを投稿しています。
表題の問題、どこが難しいのかと言いますと、場合分けですね…私に取っては。
場合分けをするときに、普通は変数 $ x $ について場合分けするのですが、この問題は定数を表す $ a $ 。
そう! $ a $ に対して場合分けをしなくてはならないところが難しい!
数回この問題の解説動画を視聴していますが、いざ自分の力で記述しようと思うと…
$ a $ の場合分けをどうやったら良いのか分からない…頭の中が真っ白、と言った感じです。
実は今日の今日まで $ a $ についての場合分けが必要である、と言うことにさえ気が付いていなかった。( ^^;
やっぱり目を見ているだけでは駄目ですね。分かった気のはなれるのですが、いざ一人で書こうとすると分からない…。
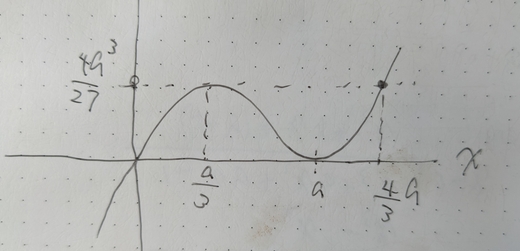
上手のように、$ f(x) $ のグラフを描いて、ポイントとなる数値までは計算できたんですけどね。
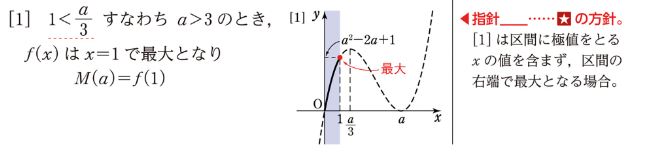
解答によると、場合分けは次にしめすように [1],[2],[3] となります。
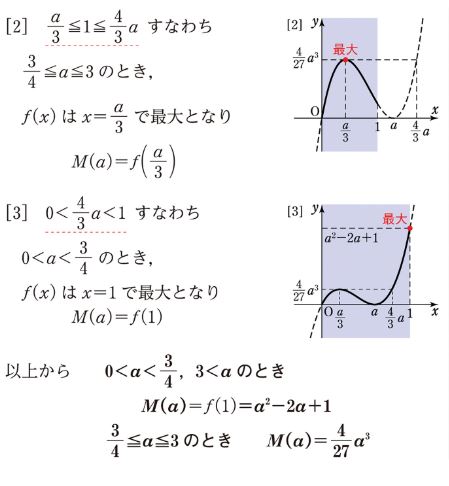
すぐさま $ a $ の範囲を記述できる方はなかなかいらっしゃらないでしょう。
まずは、$ x = 1 $ と $ a $ の関係を記述するところから入らないと分かりません。
(これを書くにも、なかなか難しかったですが)
この関係が記述できて、次にそれを $ a $ に付いての範囲に書き換えるのです。
(ここがさらに私に取っては難しい・分かりにくかった)
この場合分けを、以前にも2、3回みているのですが…
今日ノートに書き出せなかった…。_| ̄|○
この問題…自分の中では「わかった」と3回くらい思ったんですが。
明日になったら、また書けない・分かんなかったりしてね…
でも、そうならば、また明後日かけるようにするだけです…。
それと、復習のほうも実施しないとね…く、苦しい…
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
今日も朝から理想の学習スタイル (下記) を試みて、今までの自分を乗り越えようとしていたのですが…
・新たな問題の取り組み
「青チャート」の基本例題 最低1問
・復習
「青チャート」の基本例題1章分に目を通す
「青チャート」の基本例題 最低1問
・復習
「青チャート」の基本例題1章分に目を通す
お昼を過ぎ、午後の2時にやっと、表題の問題が一つ理解がでたのみです。
復習に入る前にこんなに時間が掛かってしまうなんてね…朝から午後の2時までかかっていた問題と言うのは表題のとおり
「新課程 青チャート式数学II」基本例題223 (改訂版では 213)
です。

この問題は、実は3ヶ月前から理解するのに手こずっていた問題です。
(恥ずかしながら…)
・しばらく数学の問題を解いていないことを実感…「新課程 青チャート式数学II」基本例題223
振り返ってみると、今年の7月23日に実施された数学検定2級に不参加、欠席したことに始まりますね。
受検日当日、受験会場の駐車場に空きが無かったがため、受検を断念したのですけどね。
9月30日に実施された数学検定にはなんとか出席したのですが…。
とにかく今年の7月後半から今日にかけて、どうにも数学の学習が思うように進められなくなっているんです。
今日も朝から絶不調。( ^^;
でもなんとか、今は「新課程 青チャート式数学II」基本例題223」を理解することができて、こうしてブログを投稿しています。
表題の問題、どこが難しいのかと言いますと、場合分けですね…私に取っては。
場合分けをするときに、普通は変数 $ x $ について場合分けするのですが、この問題は定数を表す $ a $ 。
そう! $ a $ に対して場合分けをしなくてはならないところが難しい!
数回この問題の解説動画を視聴していますが、いざ自分の力で記述しようと思うと…
$ a $ の場合分けをどうやったら良いのか分からない…頭の中が真っ白、と言った感じです。
実は今日の今日まで $ a $ についての場合分けが必要である、と言うことにさえ気が付いていなかった。( ^^;
やっぱり目を見ているだけでは駄目ですね。分かった気のはなれるのですが、いざ一人で書こうとすると分からない…。

上手のように、$ f(x) $ のグラフを描いて、ポイントとなる数値までは計算できたんですけどね。
解答によると、場合分けは次にしめすように [1],[2],[3] となります。


すぐさま $ a $ の範囲を記述できる方はなかなかいらっしゃらないでしょう。
まずは、$ x = 1 $ と $ a $ の関係を記述するところから入らないと分かりません。
(これを書くにも、なかなか難しかったですが)
この関係が記述できて、次にそれを $ a $ に付いての範囲に書き換えるのです。
(ここがさらに私に取っては難しい・分かりにくかった)
この場合分けを、以前にも2、3回みているのですが…
今日ノートに書き出せなかった…。_| ̄|○
この問題…自分の中では「わかった」と3回くらい思ったんですが。
明日になったら、また書けない・分かんなかったりしてね…
でも、そうならば、また明後日かけるようにするだけです…。
それと、復習のほうも実施しないとね…く、苦しい…
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(8276)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



