時空 解 さんの日記
2023
10月
26
(木)
16:00
本文
皆さん こんにちは、時空 解です。
昨日は「笑わない数学 第2シーズン」の第三回目、"結び目理論" でした。
これ、面白いですよ。
ぜひご視聴してみてください。
笑わない数学 第2シーズン 結び目理論 …「配信期限 :11/1(水) 午後11:29 まで
Wikipedia にも「結び目理論」は載っていますが…そのページを開いてみると分かると思いますが…とっつきにくい。( ^^;
とてもじゃありませんが、面白い数学の一分野、と言う印象は受けません。
でも「笑わない数学」の "結び目理論" では、その面白さがビンビンと伝わってきます。
誰もが想う素朴な疑問から入って、それを解明する方法をひも解いた先人のお話から入ります。

結び目理論が始まるきっかけが、あの物理学者、ウィリアム・トムソン氏の元素に対する分類方法からだったことも、強く興味をそそりますよね。
トムソン氏が想い描いた元素に対する分類方法。
それは
・原子の種類と結び目の種類との対応"
です。
この考え方に刺激を受け、トムソン氏の友人であったピーター・テイト氏が、結び目の研究を始めるのです。
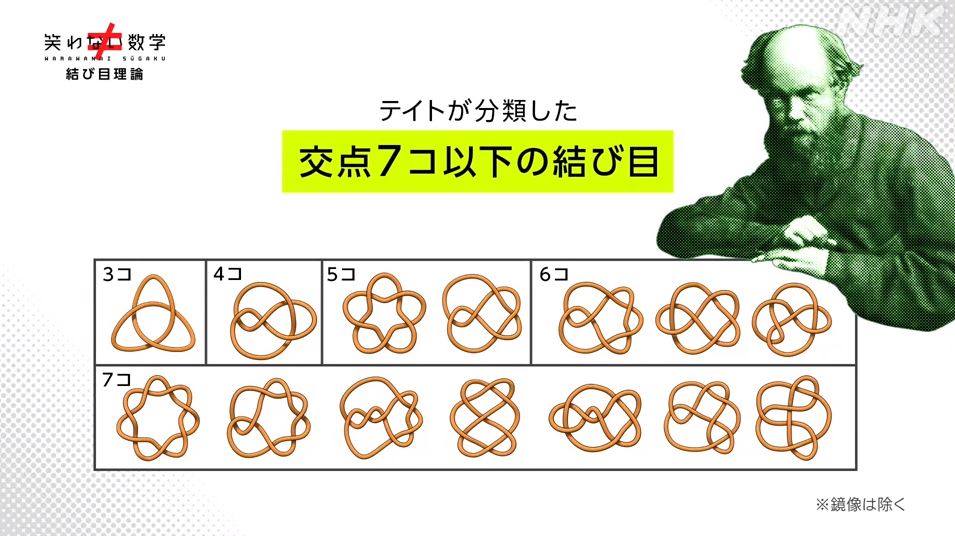
そして気の遠くなるような作業 (?) を経て、下記の結果を得ます。
・交点1コの結び目は何種類? … 0種類
・交点2コの結び目は何種類? … 105通り→0種類
・交点3コの結び目は何種類? … 10395通り→1種類
( "鏡に映した関係" を別とすると2種類)
・交点4コの結び目は何種類? … 2027025通り→1種類
・交点5コの結び目は何種類? … 654729075通り→2種類
・交点6コの結び目は何種類? … 316234143225通り→3種類
・交点7コの結び目は何種類? …213458046676875通り→7種類
こうして、まずはテイト氏がやった作業により、結び目の分類が進めらました。
取っ掛かりができれば、もう後継者は次々と現れます。
テイト氏が行ったのは分類であり、その分類を知っていても、例えば下記の結び目二つが違うものか否は判断がしにくかったんです。

しかしテイト氏が切り開いたこの分類方法に数式、のちに不変量と言う概念も持ち込んだのがジェイムズ・アレクサンダー氏でした。
・アレクサンダー多項式
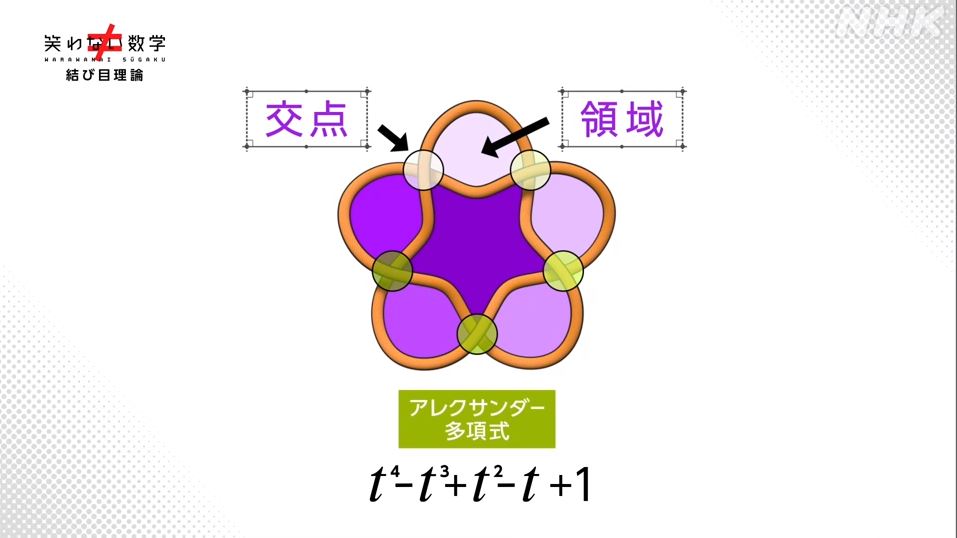
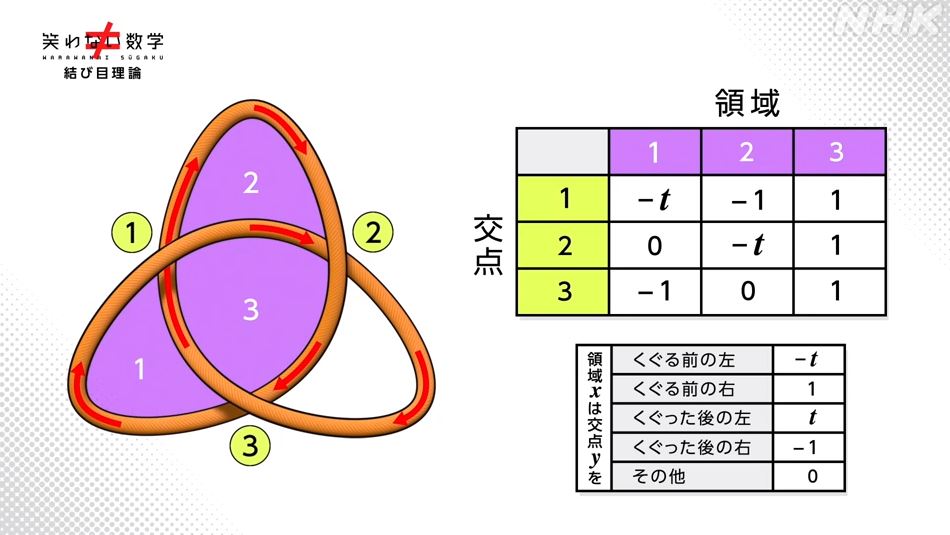
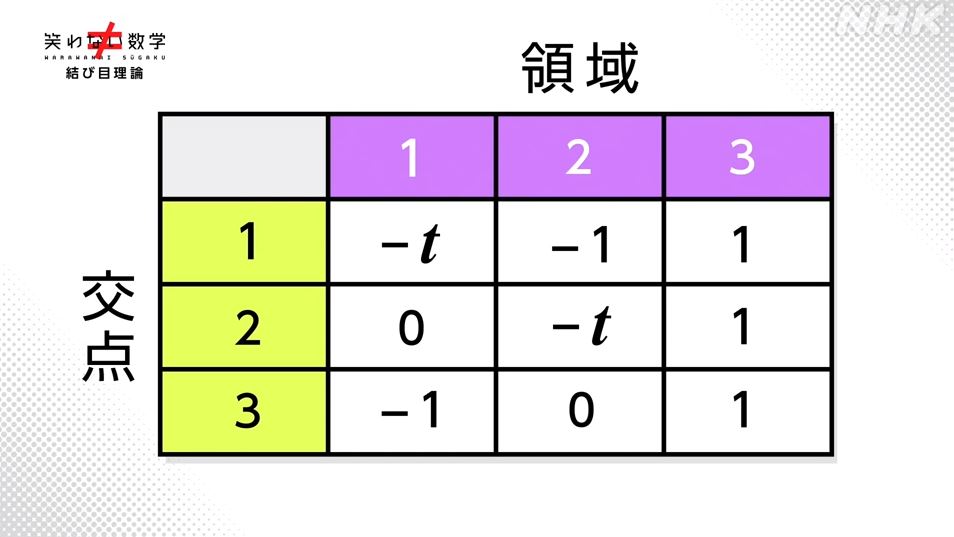



しかしこの数式にも弱点がありました。下図に示す結び目に付いて、鏡に映した関係を区別できなかったんですね。
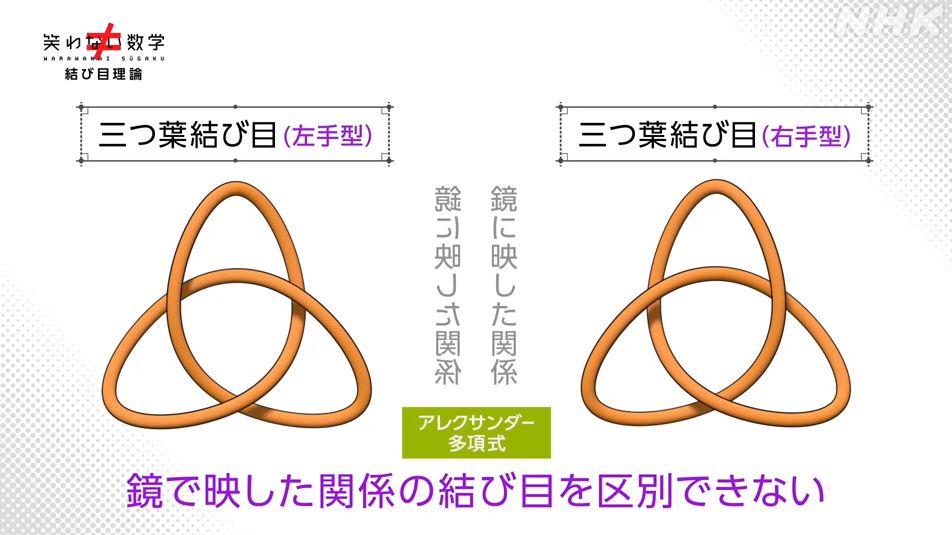
うーむ…何だかガロアの群論にも関係してそうな…してなさそうな…知的好奇心を刺激されます。
まぁガロアはともかく…
ここまでが今回の放送 "結び目理論" の放送の中で最も内容が充実していて、面白いところでしょう。
ガロアの群論には触れないものの、放送内容はアレクサンダー多項式の理解にとても有意義な解説がなされます。
Wikipedia のアレクサンダー多項式の解説は (私は) チンプンカンプンなんですけどね。
「笑わない数学 結び目理論」を視聴すると分かった気になれます。
(…まぁほんの一部分なんでしょうけど。( ^^; )
でも内容はさらに続きます。
このアレクサンダー多項式もすごいのですが、その欠点である "鏡に映した関係" をも区別する数式をヴォーン・ジョーンズ氏と言う方が 発見?発明? します。
・ジョーンズ多項式 進化した点 まだ問題が残っている点

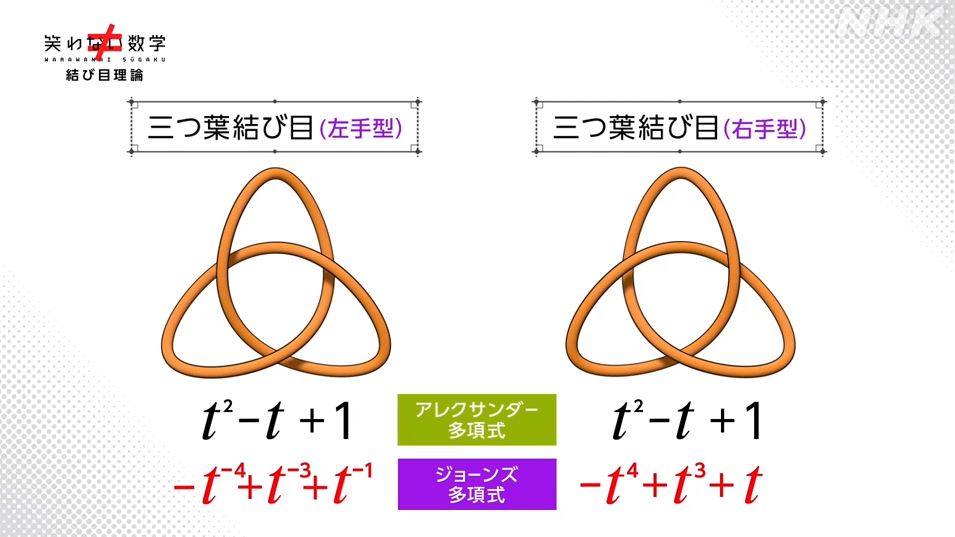
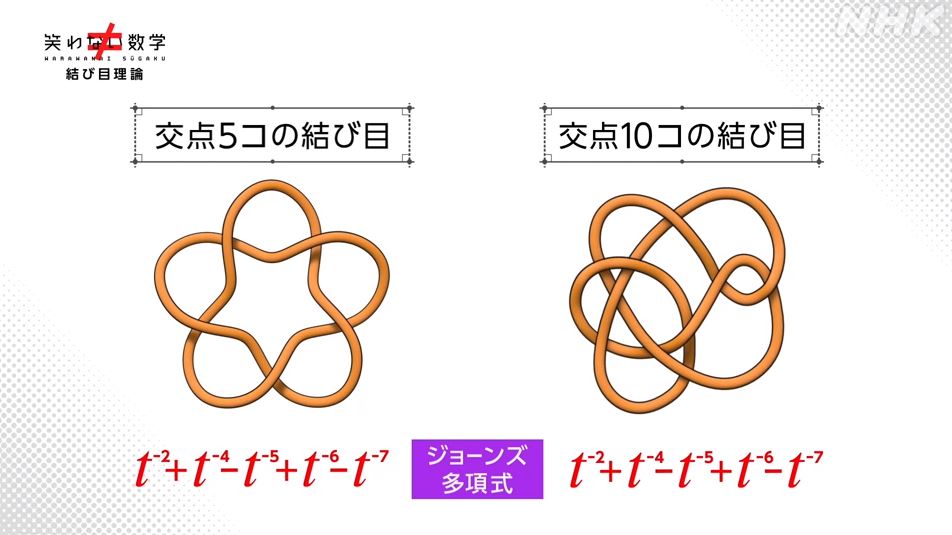
さらにジョーンズ方程式の問題点をカバーした数式
・HOMFLYPT多項式

さらにさらに進化した数式
・コンツェビッチ不変量

現在、このコンツェビッチ不変量がすべての結び目を区別できる数式なんじゃないかと期待されているそうです。
そしてこれが数学と言う分野を超え、物理学に戻ってきます!


ここも面白いですね。…でもまぁ、ちょっと強引な気もしますが…
私が高校生だったなら素直に興奮しているところでしょう。
いやぁ笑わない数学はお笑い芸人、パンサー 尾形貴弘さんが司会を務めていますが、見応えがあります。
ぜひ視聴してみてくださいね。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
昨日は「笑わない数学 第2シーズン」の第三回目、"結び目理論" でした。
これ、面白いですよ。
ぜひご視聴してみてください。
笑わない数学 第2シーズン 結び目理論 …「配信期限 :11/1(水) 午後11:29 まで
Wikipedia にも「結び目理論」は載っていますが…そのページを開いてみると分かると思いますが…とっつきにくい。( ^^;
とてもじゃありませんが、面白い数学の一分野、と言う印象は受けません。
でも「笑わない数学」の "結び目理論" では、その面白さがビンビンと伝わってきます。
誰もが想う素朴な疑問から入って、それを解明する方法をひも解いた先人のお話から入ります。

結び目理論が始まるきっかけが、あの物理学者、ウィリアム・トムソン氏の元素に対する分類方法からだったことも、強く興味をそそりますよね。
トムソン氏が想い描いた元素に対する分類方法。
それは
・原子の種類と結び目の種類との対応"
です。
この考え方に刺激を受け、トムソン氏の友人であったピーター・テイト氏が、結び目の研究を始めるのです。

そして気の遠くなるような作業 (?) を経て、下記の結果を得ます。
・交点1コの結び目は何種類? … 0種類
・交点2コの結び目は何種類? … 105通り→0種類
・交点3コの結び目は何種類? … 10395通り→1種類
( "鏡に映した関係" を別とすると2種類)
・交点4コの結び目は何種類? … 2027025通り→1種類
・交点5コの結び目は何種類? … 654729075通り→2種類
・交点6コの結び目は何種類? … 316234143225通り→3種類
・交点7コの結び目は何種類? …213458046676875通り→7種類
こうして、まずはテイト氏がやった作業により、結び目の分類が進めらました。
取っ掛かりができれば、もう後継者は次々と現れます。
テイト氏が行ったのは分類であり、その分類を知っていても、例えば下記の結び目二つが違うものか否は判断がしにくかったんです。

しかしテイト氏が切り開いたこの分類方法に数式、のちに不変量と言う概念も持ち込んだのがジェイムズ・アレクサンダー氏でした。
・アレクサンダー多項式






しかしこの数式にも弱点がありました。下図に示す結び目に付いて、鏡に映した関係を区別できなかったんですね。

うーむ…何だかガロアの群論にも関係してそうな…してなさそうな…知的好奇心を刺激されます。
まぁガロアはともかく…
ここまでが今回の放送 "結び目理論" の放送の中で最も内容が充実していて、面白いところでしょう。
ガロアの群論には触れないものの、放送内容はアレクサンダー多項式の理解にとても有意義な解説がなされます。
Wikipedia のアレクサンダー多項式の解説は (私は) チンプンカンプンなんですけどね。
「笑わない数学 結び目理論」を視聴すると分かった気になれます。
(…まぁほんの一部分なんでしょうけど。( ^^; )
でも内容はさらに続きます。
このアレクサンダー多項式もすごいのですが、その欠点である "鏡に映した関係" をも区別する数式をヴォーン・ジョーンズ氏と言う方が 発見?発明? します。
・ジョーンズ多項式 進化した点 まだ問題が残っている点



さらにジョーンズ方程式の問題点をカバーした数式
・HOMFLYPT多項式

さらにさらに進化した数式
・コンツェビッチ不変量

現在、このコンツェビッチ不変量がすべての結び目を区別できる数式なんじゃないかと期待されているそうです。
そしてこれが数学と言う分野を超え、物理学に戻ってきます!


ここも面白いですね。…でもまぁ、ちょっと強引な気もしますが…
私が高校生だったなら素直に興奮しているところでしょう。
いやぁ笑わない数学はお笑い芸人、パンサー 尾形貴弘さんが司会を務めていますが、見応えがあります。
ぜひ視聴してみてくださいね。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(7137)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



