時空 解 さんの日記
2023
11月
1
(水)
09:10
本文
皆さん こんにちは、時空 解です。
表題の通り、昨晩会社から帰宅すると、郵便ポストの A4 大の封書が入っていました。
おなじみの "合否通知" です。
おっと、来たか…まぁ楽しみにしていました。
何と言っても解けなかった問題の解答と、できたはずの問題が本当に合っているのかも知ることができるのですからね。
さて、今日は1次の結果について書いてみたいと思います。
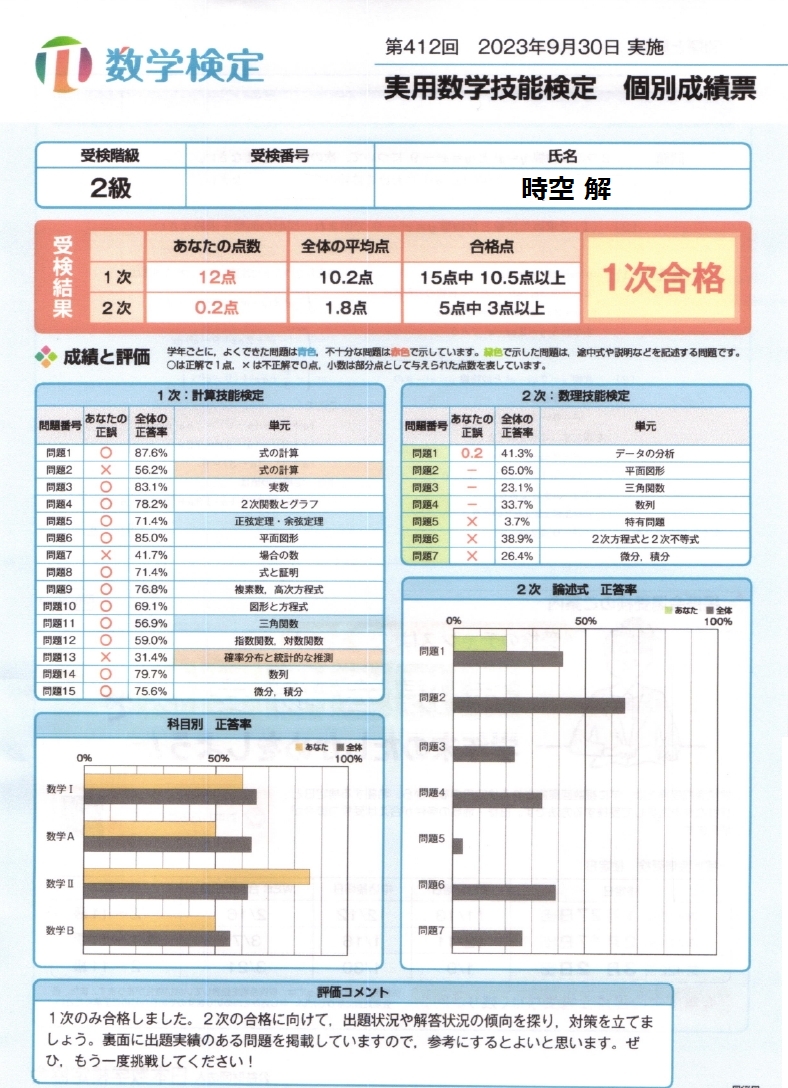
右画像に示すとおり、私は 12/15 という結果でした。
…うーむ…本当に私の苦手分野が如実に表れています。間違えた問題は3問中2問が場合の数と "確率分布" と "統計的な推測" …
でもまぁ "全体の正答率" からみても、私の間違えた3問は難しい問題だったことがわかります。
問題2の因数分解、これは初めから後回しにしたくらい取っつきにくい問題でした。
でも、今日ちょっとやってみたら分かりました。
…なるほどぁ~ やっぱり文字が3つあると見通しが悪いと言うことですかね…。
与式を下記のように整理できると、すぐに分るでしょう。
今日なら解けるのに…。
検定時は時間が気になって、$ (a+2c) $ が見通せなかったです。
いきなり与式を展開してから整理して…なんてやってたら泥沼…時間が足りなくなってしまいますよね。
冷静に問題をみるメンタルも大事です。
とりあえず今日はこんなところで…
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
表題の通り、昨晩会社から帰宅すると、郵便ポストの A4 大の封書が入っていました。
おなじみの "合否通知" です。

おっと、来たか…まぁ楽しみにしていました。
何と言っても解けなかった問題の解答と、できたはずの問題が本当に合っているのかも知ることができるのですからね。
さて、今日は1次の結果について書いてみたいと思います。
右画像に示すとおり、私は 12/15 という結果でした。
…うーむ…本当に私の苦手分野が如実に表れています。間違えた問題は3問中2問が場合の数と "確率分布" と "統計的な推測" …
でもまぁ "全体の正答率" からみても、私の間違えた3問は難しい問題だったことがわかります。
問題2の因数分解、これは初めから後回しにしたくらい取っつきにくい問題でした。
第412回 2023年 9月30日 (土) 実施 数学検定2級 1次
問題2.次の式を因数分解しなさい。
$ (a+2b +2c)(a-6b+2c) +3ab+6bc $
問題2.次の式を因数分解しなさい。
$ (a+2b +2c)(a-6b+2c) +3ab+6bc $
でも、今日ちょっとやってみたら分かりました。
…なるほどぁ~ やっぱり文字が3つあると見通しが悪いと言うことですかね…。
与式を下記のように整理できると、すぐに分るでしょう。
$ (a+2b +2c)(a-6b+2c) +3ab+6bc $
$ = \{(a+2c)+2b \}\{(a+2c)-6b \} + 3b(a+2c) $
ここで $ (a+2c) = Q $ とすると、上式は
$ (Q+2b)(Q-6b) + 3bQ $
これを展開して整理してやると
$ Q^2 -4bQ -12b^2 +3bQ $
$ = Q^2 -bQ -12b^2 $
$ =(Q +3b)(Q -4b) $
$ Q $ をもとに戻して
$ (a+2c +3b)(a+2c -4b) $
$ \underline { Ans: \textcolor{green}{ (a +3b+2c)(a -4b+2c) } } $
$ = \{(a+2c)+2b \}\{(a+2c)-6b \} + 3b(a+2c) $
ここで $ (a+2c) = Q $ とすると、上式は
$ (Q+2b)(Q-6b) + 3bQ $
これを展開して整理してやると
$ Q^2 -4bQ -12b^2 +3bQ $
$ = Q^2 -bQ -12b^2 $
$ =(Q +3b)(Q -4b) $
$ Q $ をもとに戻して
$ (a+2c +3b)(a+2c -4b) $
$ \underline { Ans: \textcolor{green}{ (a +3b+2c)(a -4b+2c) } } $
今日なら解けるのに…。
検定時は時間が気になって、$ (a+2c) $ が見通せなかったです。
いきなり与式を展開してから整理して…なんてやってたら泥沼…時間が足りなくなってしまいますよね。
冷静に問題をみるメンタルも大事です。
とりあえず今日はこんなところで…
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6278)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



