時空 解 さんの日記
2023
11月
4
(土)
09:36
本文
皆さん こんにちは、時空 解です。
今日は2次の問題の復習に入っています。
2次検定は、5点中 0.2点しか取れなかった私ですので… …_| ̄|○;
全問、7問について検討する必要があります。
今日はどこまでできるか分かりませんが、時間いっぱいやってみたいと思います。
ではまず1問目から
第412回 数学検定2級2次 問題1…(模範解答は右画像)


こんな問題、本当なら解けないといけないのですけどね。
でも、まずは当日は "分散" の定義式がうる覚えで思い出せなかったのです。
情けない。
こんなの2つの方程式 (1次方程式と2次方程式) を立てて、それを解くだけです。
・1次方程式は平均値をもとに作る式
・2次方程式は分散の公式をもとに作る式
この二つですよね。
…でもね…今日は "分散" の公式が分かっていたので (受検後、"分散" の公式を調べて記憶しておいた) 問題が解けるはずだったんですが。

いざ解いてみると、$ \displaystyle \frac{ 1 }{ n } $ が抜け落ちました。
しかも別の個所でも計算間違い…。駄目だこりゃ。
気を取り直して、第2問。
第412回 数学検定2級2次 問題2…(模範解答は右画像)


この問題も解けないといけなかった問題です。検定当日にはこの問題を見て
「あ、メネラウスの定理を使う問題だ」
とすぐに分かったんですけどね…
いざ、図にメネラウスの定理を適用しようと思ったのですが…。
どこをどう見て分数式に当て嵌めるのかごちゃごちゃになって、結局解答できず。_| ̄|○
今日見てみてもごちゃごちゃになるしまつ…
この原因は、記憶違いにありました。チェバ、メネラウスの定理の 利用方法 を記憶違いしてたのが一つ。
「頂 → 点 → 頂 で三角形をひとまわり」
これではごちゃごちゃになるよね。
正しくは
「頂 → 分 → 頂 で三角形をひとまわり」
でした。
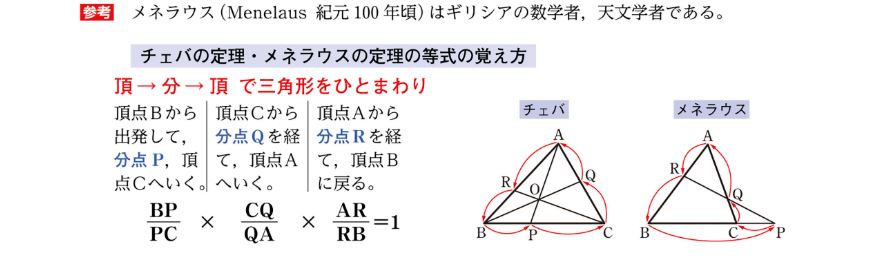
チェバの定理の方には比較的 "頂 → 分 → 頂" は適用し易いのですけどね。メネラウスの定理のほうは慣れが必要だと言うことを実感します…。
さて、後1問できそうです…
第412回 数学検定2級2次 問題3…(模範解答は右画像)


この問題は少々手ごわい問題のように思いました。
これって、
$ \cos $ 、 $ \sin $ の2種類の三角関数を1種類にする。
と言う方向性には気が付くと思いますが、でも $ \sin^2 \theta + \cos^2 \theta = 1 $ を使って一つにすると泥沼です。
これじゃないなと分かったのですが…そこで検定当日は諦めました。
この問題は "三角関数の合成" をつかうんですよね。さんざん勉強・検討した "三角関数の合成" …。
これが利用できないなんて…_| ̄|○
さらにこの問題は、ここから神経を使う問題です。最大値・最小値を求める問題ですからね。
模範解答を一度見たのに、改めて一人で解答を記述しようとしたのですが…できませんでした。
まだまだ勉強しないと、点は取れない私ですね…とほほ。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
今日は2次の問題の復習に入っています。
2次検定は、5点中 0.2点しか取れなかった私ですので… …_| ̄|○;
全問、7問について検討する必要があります。
今日はどこまでできるか分かりませんが、時間いっぱいやってみたいと思います。
ではまず1問目から
第412回 数学検定2級2次 問題1…(模範解答は右画像)


こんな問題、本当なら解けないといけないのですけどね。
でも、まずは当日は "分散" の定義式がうる覚えで思い出せなかったのです。
情けない。
こんなの2つの方程式 (1次方程式と2次方程式) を立てて、それを解くだけです。
・1次方程式は平均値をもとに作る式
・2次方程式は分散の公式をもとに作る式
この二つですよね。
…でもね…今日は "分散" の公式が分かっていたので (受検後、"分散" の公式を調べて記憶しておいた) 問題が解けるはずだったんですが。

いざ解いてみると、$ \displaystyle \frac{ 1 }{ n } $ が抜け落ちました。
しかも別の個所でも計算間違い…。駄目だこりゃ。
気を取り直して、第2問。
第412回 数学検定2級2次 問題2…(模範解答は右画像)


この問題も解けないといけなかった問題です。検定当日にはこの問題を見て
「あ、メネラウスの定理を使う問題だ」
とすぐに分かったんですけどね…
いざ、図にメネラウスの定理を適用しようと思ったのですが…。
どこをどう見て分数式に当て嵌めるのかごちゃごちゃになって、結局解答できず。_| ̄|○
今日見てみてもごちゃごちゃになるしまつ…
この原因は、記憶違いにありました。チェバ、メネラウスの定理の 利用方法 を記憶違いしてたのが一つ。
「頂 → 点 → 頂 で三角形をひとまわり」
これではごちゃごちゃになるよね。
正しくは
「頂 → 分 → 頂 で三角形をひとまわり」
でした。

チェバの定理の方には比較的 "頂 → 分 → 頂" は適用し易いのですけどね。メネラウスの定理のほうは慣れが必要だと言うことを実感します…。
さて、後1問できそうです…
第412回 数学検定2級2次 問題3…(模範解答は右画像)


この問題は少々手ごわい問題のように思いました。
これって、
$ \cos $ 、 $ \sin $ の2種類の三角関数を1種類にする。
と言う方向性には気が付くと思いますが、でも $ \sin^2 \theta + \cos^2 \theta = 1 $ を使って一つにすると泥沼です。
これじゃないなと分かったのですが…そこで検定当日は諦めました。
この問題は "三角関数の合成" をつかうんですよね。さんざん勉強・検討した "三角関数の合成" …。
これが利用できないなんて…_| ̄|○
さらにこの問題は、ここから神経を使う問題です。最大値・最小値を求める問題ですからね。
模範解答を一度見たのに、改めて一人で解答を記述しようとしたのですが…できませんでした。
まだまだ勉強しないと、点は取れない私ですね…とほほ。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6930)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



